Andrewei's Blog
0%

并查集

发表于 更新于 分类于 ，

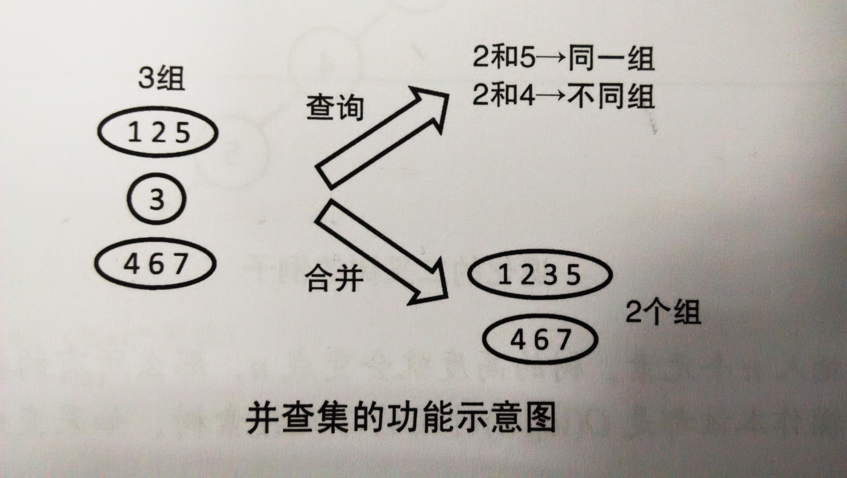
并查集

概述

并查集是一种用来管理元素分组情况的数据结构。冰茶既可以高效的进行如下操作。不过需要注意并查集虽然可以进行合并操作，但是却无法进行分割操作。 并查集可以查询元素a和元素b是否属于同一组。 并查集可以合并元素a和元素b所在的组。QQ截图20151026165823

主要操作

初始化

把每个点所在集合初始化为其自身。
通常来说，这个步骤在每次使用该数据结构时只需要执行一次，无论何种实现方式，时间复杂度均为O(N)。

1
2
3
4
5
void init(){
    int i;
    for(i = 0; i < n; i++)
        par[i] = i;
}

查找

查找元素所在的集合，即根节点。

1
2
3
4
5
int find(int x){
    if(par[x] != x)
        par[x] = find(par[x]);
    return par[x];
}

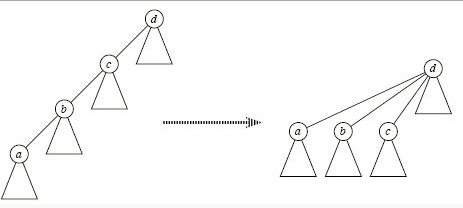
注意在这一步中通常采用路径优化，代码中 $par[x] = find(par[x])$  即采用了路径优化，做了如图所示的转化，将所有的子节点都直接挂载在根节点上，使得接下来的查找更高效。

QQ截图20151026170253

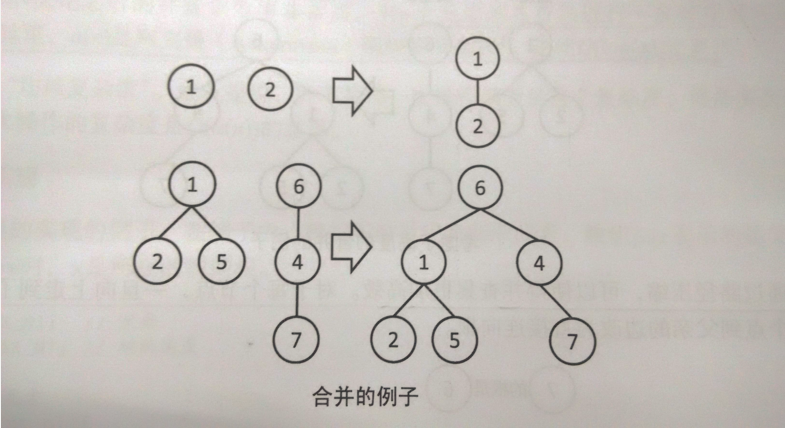
将两个元素所在的集合合并为一个集合。
通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找”操作实现。
QQ截图20151026170346

1
2
3
4
5
6
void Union(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx != fy)
        par[fy] = fx;
}

代码说明，先查找两个元素是否属于同一集合，即他们的根节点是否相同，若不相同就合并他们。

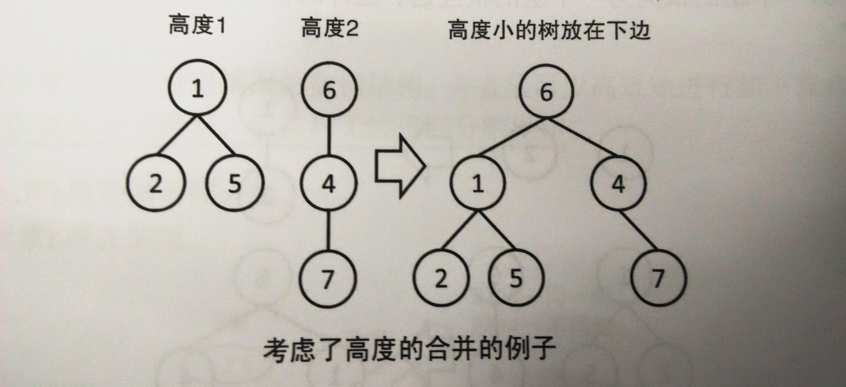
这里也可以进一步优化，对于每一个集合所形成的树，用一个rank[N] 数组来记录它的高度，合并时如果两棵树的高度不同，那么从rank 小的向rank 大的连边。
QQ截图20151026170553

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void Union(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx != fy){
        if(rank[fx] >= rank[fy]){
            par[fy] = fx;
            rank[fx]++;
        }
        else{
            par[fx] = fy;
            rank[fy]++;
        }
    }
}

复杂度分析

在增加了路径优化和合并注意高度的优化后，并查集的效率非常高。可以证明，通过这种树形结构实现的带启发式路径压缩的并查集，Find和Union操作的平均代价是O(lgn)，这和二分查找的复杂度一致，可以证明这已经是理论上最好的算法了，不可能有更好的算法了。如果不进行这种路经压缩的话，并查集就退化成了链表，在同一链表中的元素属于同一集合，这样的话Find的复杂度是O(n)。

POJ 例题分析

POJ 2524

题目大意：

有n 个数字，接下来会有m对数字，每一对数字属于同一类。
输入数据包括情况的数目，每一种情况包括有数据n和m，接下来的m行包括了两个数据i和j，表示数字i和j是同一类。数字是从1到n编号的，若n=0并且m=0则表示输入结束 对于每一种情况，显示出这n个数字的种类数。

思路分析：

并查集的初级题目，可以用根节点的rank存储这一类的元素个数，子节点的rank全置为零，这样只要看有几个rank并不为零就可以确定这n个数字的种类数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<iostream>
#define N 50005
using namespace std;

int par[N], rank[N]; //par[N] 为 i 的父节点
int n, m;

void init(){ //初始化 
    int i;
    for(i = 1; i <= n; i++){
        rank[i] = 1;
        par[i] = i;
    }
}

int find(int x){ //找根结点
    if(par[x] == x) 
        return x;
    else
        return par[x] = find(par[x]);
}

void unite(int x, int y){ //合并两个元素，同时，注意rank的处理
    x = find(x);
    y = find(y);
    if(x == y) return ;
    if(rank[x] > rank[y]){
        rank[y] = 0;
        par[y] = x;
        rank[x] ++;
    }
    else if(rank[x] < rank[y]){
        par[x] = y;
        rank[x] = 0;
        rank[y] ++;
    }
    else{
        par[y] = x;
        rank[y] = 0;
        rank[x] ++;
    }
}

int main(){
    int i, j, x, y, sum, a = 0;
    while(cin >> n >>m){
        if(n == 0 && m == 0)
            break;
        a++;
        sum = 0;
        init();
        for(i = 0; i < m; i++){
            cin >> x >> y;
            unite(x, y);
        }
        for(i = 1; i <= n; i++){ //如果rank不为零，则记为一个种类。
            if(rank[i] != 0)
                sum += 1;
        }
        cout <<"Case "<< a <<": "<< sum << endl; 
    }
    return 0;
}

POJ 1703

题目大意：

将所有的数字分为两个部分并由输入的字符来确定要做的事情，其中A 来询问后面两个数的关系，D表示后面的两个数属于不同的类别。

输入的第一行是一个字母t, 代表测试样例数目，每个测试样例的第一行包括两个数，第一个数 n 代表数字的个数（编号1~n），第二个数 m 表示接下来有m 行，每一行包括一个字符’A’或’D’表示之后两个数的关系。
对于每一个输入的’A’,输出两个数的关系,” Not sure yet.”,” In different gangs.”,” In the same gang.”

解题思路：

活用rank数组（代码中的rela数组）rank[i] = 0,表示节点 i 与根节点是同一类，rank[i] = 1表示节点 i 与根节点是不同类的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<iostream>
#include<stdio.h> 
#define N 100005
using namespace std;

int par[N], rank[N], rela[N];
int n, m;

void init(){
    int i;
    for(i = 1; i <= N; i++){
        par[i] = i;
        rela[i] = 0;
    }
}

int find(int x){
    if(par[x] == x)
        return x;
    else{
        int temp = par[x];
        par[x] = find(par[x]);
        rela[x] = (rela[temp] + rela[x]) % 2;
        // rela[x] =(rela[temp] ^ rela[x]);
        return par[x];
    }
}

void unit(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx == fy) return;
    else{
        par[fy] = fx;
        rela[fy] = (rela[x] + 1 -rela[y]) % 2;
        //rela[y] = !(rela[x] ^ rela[y]);
    }
}

void sol(int x, int y){
    if(find(x)== find(y) && rela[x] == rela[y])
        printf("In the same gang.\n"); 
    else if(find(y) == find(x) && rela[x] != rela[y])
        printf("In different gangs.\n"); 
    else 
        printf("Not sure yet.\n"); 
    return;
}

int main(){
    ios_base::sync_with_stdio(false);
    int t, i, n, x, y;
    char ch;
    scanf("%d",&t);
    while(t--){
        scanf("%d %d", &n, &m);
        init();
        for(i = 1; i <= m; i++){
            getchar();
            scanf("%c %d %d", &ch, &x, &y);
            if(ch == 'A')
                sol(x, y);
            else
                unit(x, y);
        }
    }
    return 0;
}

网上还有一种很不可思议的解法，我自己也搞不懂为什么会这样，直接上代码了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <cstdio>
#include <iostream> 
using namespace std; 
int f[200001],n,m,x,y,cas; 
char c; 
int find(int x) { 
    if (x!=f[x]) f[x] = find(f[x]); 
    return f[x]; 
} 
void Union(int x,int y) { 
    int px = find(x); 
    int py = find(y); 
    if (px != py) f[px] = py; 
} 
int main() { 
    scanf("%d",&cas); 
    while (cas--) { 
        scanf("%d%d",&n,&m); 
        for (int i=1;i<=2*n;i++) f[i] = i; 
        for (int i=1;i<=m;i++) { 
            scanf("%c%c %d %d",&c,&c,&x,&y); 
            if (c=='D') { 
                Union(x,y+n); 
                Union(y,x+n); 
            } 
            else { 
                if (find(x)==find(y)) printf("In the same gang.\n"); 
                else if (find(x)==find(y+n)||find(y)==find(x+n)) 
                    printf("In different gangs.\n"); 
                else printf("Not sure yet.\n"); 
            } 
        } 
    } 
    return 0; 
}

POJ 1182

题目大意：（直接上题吧）

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是”1 X Y”，表示X和Y是同类。
第二种说法是”2 X Y”，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

Input

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

Output

只有一个整数，表示假话的数目。

解题思路：

活用rank数组，rank[i] = 0 表示 i 与par[i] 是同类，rank[i] = 1 表示 i 吃par[i] , rank[i] = 2 表示par[i] 吃 i ；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<cstdio>
#define N 50005
using namespace std;

int par[N], rela[N]; // rela[a] == 0 表示 a 与 par[a] 同类
int n, k, a, b; // rela[a] == 1 表示 a 吃 par[a] 
// rela[a] == 2 表示 a 被 par[a] 吃
void init(){ // *******************************************************************
    int i; // 若 rela[a] == 0，rela[par[a]] == 0 -> rela[a] == 0;
    for(i = 1; i <= n; i++){ // 若 rela[a] == 0, rela[par[a]] == 1 -> rela[a] == 1;
        par[i] = i; // 若 rela[a] == 0, rela[par[a]] == 2 -> rela[a] == 2;
        rela[i] = 0; // 若 rela[a] == 1, rela[par[a]] == 0 -> rela[a] == 1;
    } // 若 rela[a] == 1, rela[par[a]] == 2 -> rela[a] == 0;
} // 若 rela[a] == 2, rela[par[a]] == 0 -> rela[a] == 2;
// 若 rela[a] == 2, rela[par[a]] == 1 -> rela[a] == 0;
int find(int x){ // 若 rela[a] == 2, rela[par[a]] == 2 -> rela[a] == 1;
    int y;
    if(par[x] == x) // 综合所有情况，可以得出结论 rela[a] = (rela[a] + rela[par[a]]) % 3;
    return x;
    y = par[x]; // ******************************************************************************
    par[x] = find(y);
    rela[x] = (rela[x] + rela[y]) % 3;
    return par[x]; // 若 d == 1, 若 rela[a] == 0, rela[b] == 0 时，rela[a] == 0;
} // (同类) rela[b] == 1 时，rela[a] == 1;
// rela[b] == 2 时，rela[a] == 2;
void unit(int x, int y, int d){ // 此处的 d 传入的实参为 d - 1; // 若 rela[b] == 0, rela[a] == 0 时，rela[a] == 0;
    int fx = find(x); // rela[a] == 1 时，rela[a] == 1;
    int fy = find(y); // rela[a] == 2 时，rela[a] == 2;
    if(fx == fy) // 若 d == 2, 若 rela[a] == 0, rela[b] == 0 时，rela[a] == 1;
    return; // (a 吃 b) rela[b] == 1 时，rela[a] == 2;
    else{ // rela[b] == 2 时，rela[a] == 0;
        par[fx] = fy; // 若 rela[b] == 0, rela[a] == 0 时，rela[a] == 1;
        rela[fx] = (rela[y] - rela[x] + d + 3) % 3; // (注意，此时的a是原a的根节点) rela[a] == 1 时，rela[a] == 0;
    } // rela[a] == 2 时，rela[a] == 2;
    return; // 综合所有情况，可以得出结论 rela[a] = (rela[b] - rela[a] + d - 1 + 3) % 3;
}
// ***********************************************************************************
int main(){
    int i, sum = 0, d, fx, fy;
    scanf("%d %d",&n,&k); 
    init();
    for(i = 1; i <= k; i++){
        scanf("%d %d %d",&d,&a,&b); 
        if(a > n || b > n ||(d == 2 && a == b))
            sum++; // 真话的条件： 当d == 1(a 与 b 同类)
        else{ // a 与 par[a] 同类，即 rela[a] == 0 时，rela[b] == 0;
            fx = find(a); // a 吃 par[a]， 即 rela[a] == 1 时，rela[b] == 1;
            fy = find(b); // a 被 par[a]吃， 即 rela[a] == 2 时，rela[b] == 2;
            if(fx == fy && ((rela[a] - rela[b] + 3) % 3 != d - 1)) // 当 d == 2(a 吃 b) 
                sum++; // a 与 par[a] 同类，即 rela[a] == 0 时，rela[b] == 2;
            else unit(a, b, d - 1); // a 吃 par[a], 即 rela[a] == 1 时，rela[b] == 0;
        } // a 被 par[a]吃， 即 rela[a] == 2 时，rela[b] == 1;
    }
    printf("%d\n",sum);
    return 0;
}