Andrewei's Blog
0%

生成树

发表于 更新于 分类于 ，

最小生成树

概述

在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得 的 w(T) 最小，则此 T 为 G 的最小生成树。
最小生成树其实是最小权重生成树的简称。 许多应用问题都是一个求无向连通图的最小生成树问题。例如：要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同；另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

性质

最小生成树的边数必然是顶点数减一，|E| = |V| - 1。
最小生成树不可以有环。
最小生成树不必是唯一的。

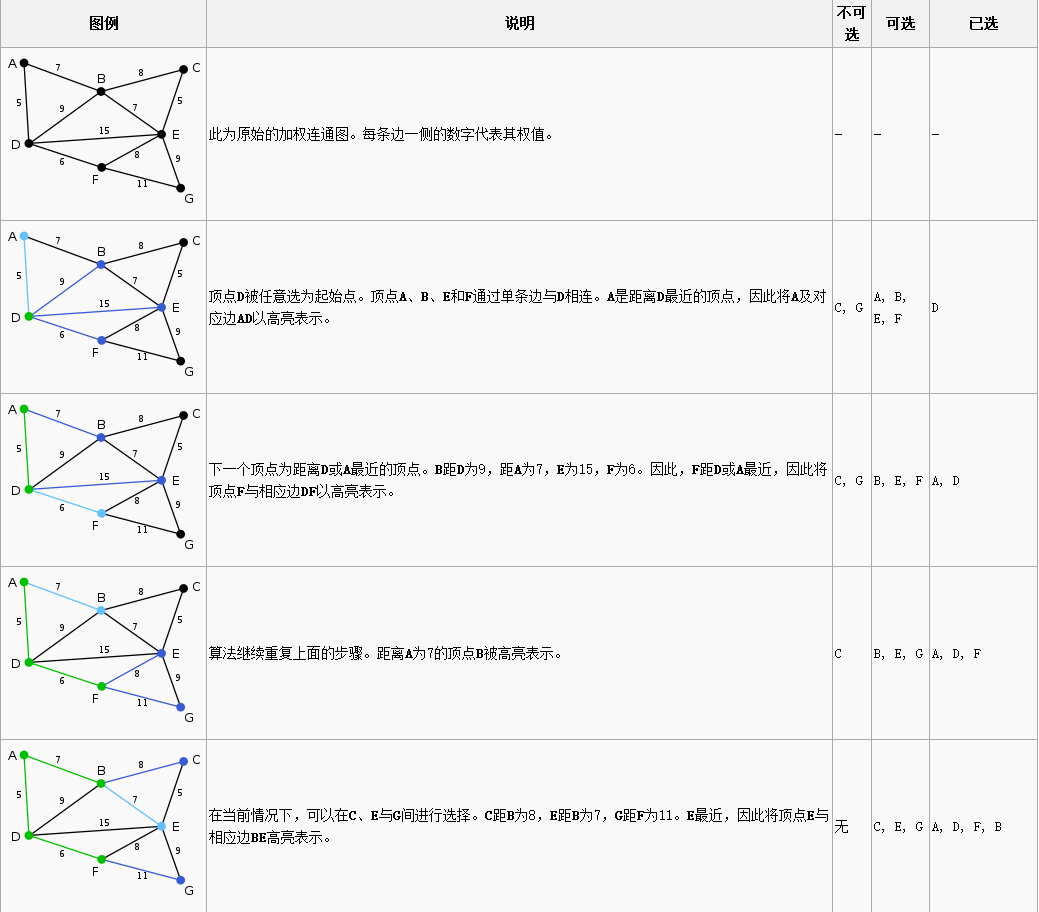
Prim 算法

描述

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克发现；并在1957年由美国计算机科学家罗伯特·普里姆独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

主要操作

从单一顶点开始，Prim算法按照以下步骤逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。
输入：一个加权连通图，其中顶点集合为V，边集合为E；
初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {}；
重复下列操作，直到Vnew = V：
在集合E中选取权值最小的边（u, v），其中u为集合Vnew中的元素，而v则不是（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
将v加入集合Vnew中，将（u, v）加入集合Enew中；

输出：使用集合Vnew和Enew来描述所得到的最小生成树。过程如图所示：

01d8ed9a66f30951a25ef99a948a

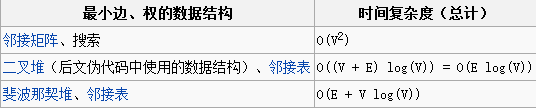
复杂度分析

通过邻接矩阵图表示的简易实现中，找到所有最小权边共需O（V2）的运行时间。使用简单的二叉堆与邻接表来表示的话，普里姆算法的运行时间则可缩减为O(E log V)，其中E为连通图的边数，V为顶点数。如果使用较为复杂的斐波那契堆，则可将运行时间进一步缩短为O(E + V log V)，这在连通图足够密集时（当E满足Ω（V log V）条件时），可较显著地提高运行速度。
c7fb458bbac68eaaacb3f01fd78f

两种实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#define N 10000
#define M 0x3f3f3f3f
int n; // n 是点的数目；
int map[N][N], low[N], div[N]; // map[N][N] 存储点和权值，low[N]中存储未收录到树的
int prim(){ // 点到树的最小距离，div记录已经收录到树中的点。
    int i, j, min, minp, sum = 0;
    for(i = 0; i < n; i++) // 初始化div[N] 数组的值 0 为未收录该点，1 为收录。
        div[i] = 0;
    div[0] = 1;
    minp = 0;
    for(i = 1; i < n; i++) // 第一次初始化low[N] 数组，存储个点到minp的距离
        low[i] = map[minp][i];
    for(i = 1; i < n; i++){
        min = M;
        for(j = 0; j < n; j++)
            if(div[j] == 0 && min > low[j]){ // 找出距离minp 最小的点，用minp记录，并记距离
                min = low[j];
                minp = j;
            }
        div[minp] = 1; // 上一个过程中找到的点被收录到树中，并加上权值
        sum += min;
        for(j = 0; j < n; j++){ // 更新low[N] 数组，使其始终保持未收录到树中的点
            if(div[j] == 0 && low[j] > map[minp][j]) // 到树的最小距离。
                low[j] = map[minp][j];
        }
    }
    return sum;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <queue>
#include <cstdio>
#include <iostream>
#define N 100
#define M (1 << 30)
using namespace std;

struct Edge{
    int v, w, n;
};
struct Node{
    int v, w;

    friend bool operator < (const Node &a, const Node &b){
        return a.w > b.w;
    }
};

int head[N], dis[N], n, m, e;
bool vis[N];
Edge edge[N * N / 2];
priority_queue < Node > que;

void init(){
    e = 0;
    while(!que.empty()) que.pop();
    fill(head, head + N, -1);
    fill(dis, dis + N, M);
    fill(vis, vis + N, false);
}

void addedge(int u, int v, int w){
    edge[e].v = v;
    edge[e].w = w;
    edge[e].n = head[u];
    head[u] = e++;
}

int prime(){
    int ans = 0;
    Node t;
    t.v = 1;
    t.w = 0;
    que.push(t);
    int nume = 0;
    while(!que.empty() && nume <= m){
        t = que.top();
        que.pop();
        if(vis[t.v]) continue;
        ans += t.w;
        vis[t.v] = true;
        nume++;
        for(int i = head[t.v]; i != -1; i = edge[i].n)
            if(!vis[edge[i].v]){
                Node tt;
                tt.v = edge[i].v;
                tt.w = edge[i].w;
                que.push(tt);
            }
    }
    If(nume == n) return ans;
    return -1;
}

int main(){
    while(scanf("%d", &n) != EOF && n){
        scanf("%d", &m);
        init();
        int a, b, w;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &a, &b, &w);
            addedge(a, b, w);
            addedge(b, a, w);
        }
        printf("%d\n", prime());
    }
    return 0;
}

Kruskal 算法

描述

假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

主要操作
  1. 记Graph中有v个顶点，e个边
  2. 新建图Graphnew，Graphnew中拥有原图中相同的e个顶点，但没有边
  3. 将原图Graph中所有e个边按权值从小到大排序
  4. 循环：从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中
    if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中添加这条边到图Graphnew中；
    过程如图所示：

67be1993566a793b82d315be6b9d
32d28b1ccb75847eda177a2acae0

复杂度分析

从Kruskal算法中可以看到，执行该算法时间主要花费在堆排序和单层循环上，而循环是线性级的，则可以认为时间复杂性主要花费在堆排序上，由堆排序算法可知，Kruskal算法的时间复杂度为O(eloge)，其中e为图的边数。

代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#define M 10000 // M 为最多的点的数目
struct maps{ // 定义新类型，maps x，y代表两个点，w为他们的权值；
    int x, y, w;
};

maps map[M * M];
int par[M], n, ne; // n 为实际点的数目，ne为两个不同的点构成的边的数目

bool cmp(const maps& a, const maps& b){ // sort 函数调用将边按权值由小到大排序
    return a.w < b.w;
}

void init(){ // 以下为并查集内容
    int i;
    for(i = 1; i <= n; i++)
        par[i] = i;
}

int find(int x){
    if(par[x] != x)
        par[x] = find(par[x]);
    return par[x];
}

bool unit(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx != fy){
        par[fy] = fx;
        return true;
    }
    return false;
}

int kruscal(){
    int i, sum = 0;
    b = 0; // b为加入树中的边的数目；
    sort(map, map + ne, cmp); // 排序；
    for(i = 1; i <= ne; i++){
        if(unit(map[i].x, map[i].y)){ // 当两点至少有一个未收录到树中时，向树中加入该边
            sum += map[i].w; // 这样做是为了防止树中出现环路；
            b++;
            if(b == n - 1) // 当边数比点数少1时，所有的点被收录到树中；
                break;
        }
    }
    return sum;
}
POJ 例题分析

POJ 1751

题目大意：一个有n个城市的国家，已知有些城市有道路联通，问增加哪些道路使得所有的城市都可以彼此联通且代价最小，已经代价是两个城市坐标的笛卡尔距离；
输入：n 表示有九个点，接下来n行将输入这就个点的坐标，之后会有一个整数q代表已经有q条边连接，接下来q行将输入这q条边所连接的点（例如： 1 2 代表上面所输入的n个坐标的第一个和第二个点已经连接。
输出：输出还需要连接的点，用空格隔开（已经连号的点不能输出）。

解题思路：Prim 算法，因为这道题目已经有一些边连起来了，故在初始化map数组时，连起来的边要置为零，由于该题要求输出被连接的两个点，在算法内部可以用一个数组来记录当前正在验证的边的端点，此外，已经连接的点不能输出，故当权值为零时则不输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<iostream>
#include<iomanip>
#define M 800
#define MAXINT 1<<28
using namespace std;

struct a{ // 定义结构体来存放点的坐标；
    int x , y;
};

int map[M][M], low[M];
int vis[M], p[M]; // 数组 P 用来存放 low 数组中权值所对应的点
int n, q;
a s[M];

void prim(){
    int i, j, minp, f = 0; // f用来标记权值是否为零；
    int min;
    for(i = 1; i <= n; i++)
        vis[i] = 0;
    vis[1] = 1;
    minp = 1;
    for(i = 2; i <= n; i++){
        p[i] = minp; // p 数组用来存放 low 数组中的权值所对应的点
        low[i] = map[minp][i];
    }
    for(i = 1; i < n; i++){
        min = MAXINT;
        for(j = 1; j <= n; j++)
            if(vis[j] == 0 && min > low[j] && minp != j){ // minp != j 即跳过边的两端为同一个点的情况
                minp = j;
                min = low[j];
                if(map[p[j]][minp] == 0) // 若权值为零，则标记下来；
                    f = 1;
                else
                    f = 0;
            }
        vis[minp] = 1;
        if(f == 0) // 权值为零时不输出；
            cout<< p[minp] <<" "<< minp <<endl;
        mina = minp;
        for(j = 1; j <= n; j++)
            if(vis[j] == 0 && map[minp][j] < low[j]){
                p[j] = minp;
                low[j] = map[minp][j];
            }
    }
}
int main(){
    int i, j, a, b;
    int l;
    cin >> n;
    for(i = 1; i <= n; i++)
        cin >> s[i].x >> s[i].y;
    for(i = 1; i <= n; i++){
        for(j = 1; j <= n; j++){
            l = (s[i].x - s[j].x) * (s[i].x - s[j].x) + (s[i].y - s[j].y) * (s[i].y - s[j].y);
            map[i][j] = map[j][i] = l; // 注意无向图应该两个方向的值相同；
        }
    }
    cin >> q;
    for(i = 1; i <= q; i++){
        cin >> a >> b;
        map[a][b] = map[b][a] = 0; // 已经连起来的边权值为零；
    }
    prim();
    return 0;
}

Kruskal 算法,注意在本题上的使用技巧，题目要求不输出已经连接的边的端点，故可以在初始化的时候将连接好的端点加入集合中，这样在kruskal算法执行过程中就不会涉及到那些边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<cstdio>
#include<stdio.h>
#include<algorithm>
#include<iostream>
#define N 755
using namespace std;

struct maps{
    int x, y, w;
};

struct s{ // 存储点的坐标
    int x, y;
};

bool cmp(const maps& a, const maps& b){
    return a.w < b.w;
}

maps map[N * N];
s s[N];
int par[N];
int n, ne, b;

void init(){
    int i;
    for(i = 1; i <= n; i++)
        par[i] = i;
}

int find(int x){
    if(par[x] != x)
        par[x] = find(par[x]);
    return par[x];
}

bool unit(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx != fy){
        par[fy] = fx;
        return true;
    }
    return false;
}

void kruscal(){
    int i, sum = 0;
    b = 0;
    sort(map, map + ne, cmp);
    for(i = 1; i <= ne; i++){
        if(unit(map[i].x, map[i].y)){
            cout << map[i].x << " " << map[i].y << endl;
            b++;
            if(b == n - 1)
                break;
        }
    }
}

int main(){
    int i, j, l, q, a;
    ne = 0;
    ios_base::sync_with_stdio(false);
    cin >> n;
    init();
    for(i = 1; i <= n; i++)
        cin >> s[i].x >> s[i].y;
    for(i = 1; i <= n; i++)
        for(j = 1; j <= n; j++)
            if(i != j){ // 避免重（chong）点
                l = (s[i].x - s[j].x) * (s[i].x - s[j].x) + (s[i].y - s[j].y) * (s[i].y - s[j].y);
                map[ne].x = i;
                map[ne].y = j;
                map[ne].w = l;
                ne++;
            }
    cin >> q;
    for(i = 0; i < q; i++){
        cin >> a >> b;
        par[find(b)] = par[find(a)]; // 已经连起来的边的端点收录到集合中；
        b++; // 记录边的条数；
    }
    kruscal();
    return 0;
}

POJ 2966

题目大意：一个图中有几个连通分支（并不是每个点与其他点都有连接，只有一部分边） 。你可以连通任意两个点。求在满足使这个图成为连通图的前提下，使你所连的两点间的边的sum(权值)最小。
输入：第一行为case个数，每个case里的第一行为两个数N和E分别表示点的个数和边的条数，接下来的E行是两个点和他们的权值。
输出：每个case输出一行，即连接这些点的最小权值。
解题思路: Prim 算法，最小生成树最基本的题目，只要把map数组初始化为很大的值，就可以在程序运行中避开那些不能连接的边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#define M 505
#define MAXINT 1000
using namespace std;

int map[M][M], low[M], vis[M];
int t, e, n;

void prim(){
    int i, j, min, minp, key = 0;
    min = MAXINT;
    for(i = 0; i < n; i++)
        vis[i] = 0;
    vis[0] = 1;
    minp = 0;
    for(i = 0; i < n; i++)
        low[i] = map[minp][i];
    for(i = 0; i < n - 1; i++){
        min = MAXINT;
        for(j = 0; j < n; j++)
            if(min > low[j] && vis[j] == 0){
                min = low[j];
                minp = j;
            }
        key += min;
        vis[minp] = 1;
        for(j = 0; j < n; j++)
            if(vis[j] == 0 && map[minp][j] < low[j])
                low[j] = map[minp][j];
    }
    cout<< key <<endl;
}

int main(){
    ios_base::sync_with_stdio(false);
    int i, j, k, c;
    cin >> t;
    while(t--){
        for(i = 0; i < M; i++)
            for(j = 0; j < M; j++)
                map[i][j] = MAXINT; // 初始化为很大的值
        cin >> n >> e;
        for(k = 0; k < e; k++){
            cin >> i >> j;
            cin >> c;
            map[j][i] = map[i][j] = c;
        }
        prim();
    }
    return 0;
}

Kruskal 算法：没技巧，直接套模版。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<iostream>
#include<algorithm>
#include<cstdio>
#define N 505
using namespace std;

struct maps{
    int x, y, w;
};

maps map[N * N];
int par[N], n, e;

bool cmp(const maps& a, const maps& b){
    return a.w < b.w;
}

void init(){
    int i;
    for(i = 0; i <= n; i++){
        par[i] = i;
    }
}

int find(int x){
    if(par[x] != x)
        par[x] = find(par[x]);
    return par[x];
}

bool unit(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx != fy){
        par[fy] = fx;
        return true;
    }
    return false;
}

void kruscal(){
    int i, b = 0, sum = 0;
    init();
    sort(map, map + e, cmp);
    for(i = 0; i < e; i++)
        if(unit(map[i].x, map[i].y)){
            sum += map[i].w;
            b++;
            if(b == n - 1){
                printf("%d\n", sum);
                break;
            }
        }
}

int main(){
    int i, j, t, x, y, cost;
    scanf("%d", &t);
    while(t--){
        scanf("%d %d", &n, &e);
        for(i = 0; i < e; i++){
            scanf("%d %d %d", &x, &y, &cost);
            map[i].x = x;
            map[i].y = y;
            map[i].w = cost;
        }
        kruscal();
    }
    return 0;
}

次小生成树（k小生成树）

概述

给出一个带边权的无向图G，设其最小生成树为T，求出图G的与T不完全相同的边权和最小的生成树（即G的次小生成树）。一个无向图的两棵生成树不完全相同，当且仅当这两棵树中至少有一条边不同。注意，图G可能不连通，可能有平行边，但一定没有自环（其实对于自环也很好处理：直接舍弃。因为生成树中不可能出现自环）。定义生成树T的一个可行变换(-E1, +E2)：将T中的边E1删除后，再加入边E2（满足边E2原来不在T中但在G中），若得到的仍然是图G的一棵生成树，则该变换为可行变换，该可行变换的代价为(E2权值 - E1权值)。这样，很容易证明，G的次小生成树就是由G的最小生成树经过一个代价最小的可行变换得到。进一步可以发现，这个代价最小的可行变换中加入的边E2的两端点如果为V1和V2，那么E1一定是原来最小生成树中从V1到V2的路径上的权值最大的边。

prim算法

描述

设立数组F，F[x][y]表示T中从x到y路径上的最大边的权值。F数组可以在用Prim算法求最小生成树的过程中得出。每次将边(i, j)加入后（j是新加入树的边，i=c[j]），枚举树中原有的每个点k（包括i，但不包括j），则F[k][j]=max{F[k][i], (i, j)边权值}，又由于F数组是对称的，可以得到F[j][k]=F[k][j]。然后千万记住将图G中的边(i, j)删除（就是将邻接矩阵中(i, j)边权值改为∞）！因为T中的边是不能被加入的。等T被求出后，所有的F值也求出了，然后，枚举点i、j，若邻接矩阵中边(i, j)权值不是无穷大（这说明i、j间存在不在T中的边），则求出{(i, j)边权值 - F[i][j]}的值，即为加入边(i, j)的代价，求最小的总代价即可。

另外注意三种特殊情况：

  1. 图G不连通，此时最小生成树和次小生成树均不存在。判定方法：在扩展T的过程中找不到新的可以加入的边；
  2. 图G本身就是一棵树，此时最小生成树存在（就是G本身）但次小生成树不存在。判定方法：在成功求出T后，发现邻接矩阵中的值全部是无穷大；
  3. 图G存在平行边。这种情况最麻烦，因为这时代价最小的可行变换(-E1, +E2)中，E1和E2可能是平行边！
    因此，只有建立两个邻接矩阵，分别存储每两点间权值最小的边和权值次小的边的权值，然后，每当一条新边(i, j)加入时，不是将邻接矩阵中边(i, j)权值改为无穷大，而是改为连接点i、j的权值次小的边的权值。
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <ctime>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define M (1 << 30)
#define N 2010
using namespace std;

int mp[N][N], mp1[N][N], ma[N][N], pre[N], dis[N], n, m, ans, res;
bool vis[N]; //mp1 存储次小边，ma存储每一条路径的最大值 pre 前驱

void init(){
    fill(mp[0], mp[N], M);
    fill(mp1[0], mp1[N], M);
    fill(ma[0], ma[N], 0);
    fill(dis, dis + N, M);
    fill(vis, vis + N, false);
    scanf("%d%d", &n, &m);
    int u, v, w;
    for(int i = 0; i < m; i++){
        scanf("%d%d%d", &u, &v, &w);
        if(w < mp[u][v]){
            mp1[u][v] = mp[u][v];
            mp[u][v] = w;
            mp1[v][u] = mp1[u][v];
            mp[v][u] = mp[u][v];
        }else if(w < mp1[u][v]){
            mp1[u][v] = w;
            mp1[v][u] = mp1[u][v];
        }
    }
}

int prim(int s){
    ans = 0, res = M;
    int mi, mip;
    for(int i = 1; i <= n; i++){
        dis[i] = mp[s][i];
        pre[i] = s;
    }
    vis[s] = true;
    for(int i = 1; i < n; i++){
        mi = M, mip = 0;
        for(int j = 1; j <= n; j++){
            if(!vis[j] && dis[j] < mi){
                mi = dis[j];
                s = pre[j];
                mip = j;
            }
        }
        if(mi == M) return 0; // 返回 0 时，说明不存在最小生成树
        ans += mi;
        vis[mip] = true;
        mp[s][mip] = M;
        mp[mip][s] = M;
        if(mp1[s][mip] < M && mp1[s][mip] - mi < res)
            res = mp1[s][mip] - mi;
        for(int j = 1; j <= n; j++)
            if(!vis[j] && dis[j] > mp[mip][j]){
                dis[j] = mp[mip][j];
                pre[j] = mip;
            }
        for(int j = 1; j <= n; j++)
            if(vis[j] && j != s && j != mip){
                ma[j][mip] = max(ma[j][s], mi);
                ma[mip][j] = ma[j][mip];
            }
    }
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(i != j && mp[i][j] != M)
                res = min(res, mp[i][j] - ma[i][j]);
    if(res == M) return 1; // 返回 1 时， 说明不存在次小生成树
    res += ans; // 之前的 res 都代表 E2-E1
    return 2; // 返回 2 时， 说明存在次小生成树
}

int main(){
    int t;
    //clock_t start = clock();
    scanf("%d", &t);
    for(int i = 1; i <= t; i++){
        init();
        int ch = prim(1);
        printf("Case %d: ", i);
        if(ch == 0) printf("-1\n");
        else if(ch == 1) printf("%d %d\n", ans, -1);
        else printf("%d %d\n", ans, res);
    }
    //clock_t stop = clock();
    //printf("Time = %.2lfMS\n", (double)(stop - start) / CLOCKS_PER_SEC * 1000);
    return 0;
}

Kruskal算法

描述

Kruskal算法也可以用来求次小生成树。在准备加入一条新边(a, b)（该边加入后不会出现环）时，选择原来a所在连通块（设为S1）与b所在连通块（设为S2）中，点的个数少的那个（如果随便选一个，最坏情况下可能每次都碰到点数多的那个，时间复杂度可能增至O(NM)），找到该连通块中的每个点i，并遍历所有与i相关联的边，若发现某条边的另一端点j在未选择的那个连通块中（也就是该边(i, j)跨越了S1和S2）时，就说明最终在T中”删除边(a, b)并加入该边”一定是一个可行变换，且由于加边是按照权值递增顺序的，(a, b)也一定是T中从i到j路径上权值最大的边，故这个可行变换可能成为代价最小的可行变换，计算其代价为[(i, j)边权值 - (a, b)边权值]，取最小代价即可。注意，在遍历时需要排除一条边，就是(a, b)本身（具体实现时由于用DL边表，可以将边(a, b)的编号代入）。另外还有一个难搞的地方：如何快速找出某连通块内的所有点？方法：由于使用并查集，连通块是用树的方式存储的，可以直接建一棵树（准确来说是一个森林），用“最左子结点+相邻结点”表示，则找出树根后遍历这棵树就行了，另外注意在合并连通块时也要同时合并树。

对于三种特殊情况：

  1. 图G不连通。判定方法：遍历完所有的边后，实际加入T的边数小于(N-1)；
  2. 图G本身就是一棵树。判定方法：找不到这样的边(i, j)；
  3. 图G存在平行边。这个对于Kruskal来说完全可以无视，因为Kruskal中两条边只要编号不同就视为不同的边。
    其实Kruskal算法求次小生成树还有一个优化：每次找到边(i, j)后，一处理完这条边就把它从图中删掉，因为当S1和S2合并后，(i, j)就永远不可能再是可行变换中的E2了。
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include <iostream>
#include <stdlib.h>
using namespace std;
#define re(i, n) for (int i=0; i<n; i++)
#define re3(i, l, r) for (int i=l; i<=r; i++)
const int MAXN = 7000, MAXM = 130000, INF = ~0U >> 2;

struct edge {
    int a, b, len, pre, next;
} ed[MAXM + MAXM];

struct edge2 {
    int a, b, len, No;
} ed2[MAXM];

int n, m = 0, m2, u[MAXN], ch[MAXN], nx[MAXN], q[MAXN], res1 = 0, res2 = INF;

void init_d(){
    for(int i - 0; i < n; i++){
        ed[i].a = ed[i].pre = ed[i].next = i;
        if (n % 2) m = n + 1;
        else m = n;
    }
}

void add_edge(int a, int b, int l) {
    ed[m].a = a; ed[m].b = b; ed[m].len = l; ed[m].pre = ed[a].pre; ed[m].next = a; ed[a].pre = m; ed[ed[m].pre].next = m++;
    ed[m].a = b; ed[m].b = a; ed[m].len = l; ed[m].pre = ed[b].pre; ed[m].next = b; ed[b].pre = m; ed[ed[m].pre].next = m++;
}

void del_edge(int No){
    ed[ed[No].pre].next = ed[No].next;
    ed[ed[No].next].pre = ed[No].pre;
    ed[ed[No ^ 1].pre].next = ed[No ^ 1].next;
    ed[ed[No ^ 1].next].pre = ed[No ^ 1].pre;
}

void init() {
    scanf("%d%d", &n, &m2);
    if (!m2) {
        if (n > 1) res1 = -INF;
        res2 = -INF;
        return;
    }
    init_d();
    int a, b, len;
    for(int i = 0; i < m2; i++){
        scanf("%d%d%d", &a, &b, &len);
        ed2[i].No = m; add_edge(--a, --b, len);
        ed2[i].a = a; ed2[i].b = b; ed2[i].len = len;
    }
}

int cmp(const void *s1, const void *s2) {
    return ((edge2 *)s1)->len - ((edge2 *)s2)->len;
}

void prepare() {
    for(int i = 0; i < n; i++){
        u[i] = ch[i] = nx[i] = -1;
        qsort(ed2, m2, 16, cmp);
    }
}

int find(int x){
    int r = x, r0 = x, tmp;
    while (u[r] >= 0) r = u[r];
    while (u[r0] >= 0) {
        tmp = u[r0];
        u[r0] = r;
        r0 = tmp;
    }
    return r;
}

void uni(int r1, int r2, int No, int l0) {
    q[0] = r1;
    int j, k, l1, front, rear;
    for (front = 0, rear = 0; front <= rear; front++) {
        j = ch[q[front]];
        while (j != -1) {
            q[++rear] = j;
            j = nx[j];
        }
    }
    for(int i = 0; i <= rear; i++){
        j = q[i];
        for (int p=ed[j].next; p != j; p=ed[p].next) {
            k = ed[p].b;
            if (p != No && find(k) == r2) {
                l1 = ed[p].len - l0;
                if (l1 < res2) res2 = l1;
                del_edge(p);
            }
        }
    }
    u[r2] += u[r1]; u[r1] = r2; nx[r1] = ch[r2]; ch[r2] = r1;
}

void solve() {
    int r1, r2, l0, num = 0;
    for(int i = 0; i < m2; i++){
        r1 = find(ed2[i].a);
        r2 = find(ed2[i].b);
        if (r1 != r2) {
            l0 = ed2[i].len;
            res1 += l0;
            num++;
            if (u[r1] >= u[r2]) uni(r1, r2, ed2[i].No, l0);
            else uni(r2, r1, ed2[i].No ^ 1, l0);
        }
    }
    if (num < n - 1) {
        res1 = res2 = -INF;
        return;
    }
    if (res2 == INF) res2 = -INF;
    else res2 += res1;
}

void pri() {
    printf("Cost: %d\nCost: %d\n", res1 == -INF ? -1 : res1, res2 == -INF ? -1 : res2);
}

int main() {
    init();
    if (!res1 && res2 == INF) {
        prepare();
        solve();
    }
    pri();
    return 0;
}
另解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
#include <ctime>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define N 100100
#define M (1 << 29)
#define Max(a, b) (a > b ? a : b)
using namespace std;

struct Edge{
    int a, b, w;
    friend bool operator < (const Edge &a, const Edge &b){
        return a.w < b.w;
    }
};
class LCA{
    public:
        struct Edge{
            int v, n, w;
            void init(int a, int b, int c){
                v = a, n = b, w = c;
            }
        };
        Edge tedge[2 * N], qedge[2 * N], aedge[2 * N];
        int thead[N], qhead[N], ahead[N];
        int vis[N], par[N], ma[2 * N], ans[2 * N];
        int te, qe, ae;

        void init(){
            te = qe = ae = 0;
            fill(ma, ma + 2 * N, -M);
            for(int i = 0; i < N; i++){
                par[i] = i;
                thead[i] = qhead[i] = ahead[i] = -1;
                //ma[i] = -M;
                vis[i] = false;
            }
        }

        int find(int x){
            int temp = par[x];
            if(x != temp) par[x] = find(par[x]);
            ma[x] = Max(ma[x], ma[temp]);
            return par[x];
        }

        void addEdge(int *head, Edge *edge, int u, int v, int w, int &e){
            edge[e].v = v, edge[e].w = w, edge[e].n = head[u], head[u] = e++;
            if(head == ahead) return;
            edge[e].v = u, edge[e].w = w, edge[e].n = head[v], head[v] = e++;
        }

        void dfs(int a){
            vis[a] = 1;
            for(int i = qhead[a]; i + 1; i = qedge[i].n){
                int b = qedge[i].v;
                if(vis[b]){
                    int temp = find(b);
                    addEdge(ahead, aedge, temp, a, i, ae);
                }
            }
            for(int i = thead[a]; i + 1; i = tedge[i].n){
                int b = tedge[i].v;
                if(vis[b] == 0){
                    dfs(b);
                    par[b] = a;
                    ma[b] = tedge[i].w;
                }
            }
            for(int i = ahead[a]; i + 1; i = aedge[i].n){
                int x = aedge[i].v;
                int t = aedge[i].w;
                int y = qedge[t].v;
                find(x);
                find(y);
                ans[qedge[t].w] = Max(ma[x], ma[y]);
            }
        }
}lca;

int par[N], n, m;
Edge edge[2 * N];
bool vis[N];

void init(){
    for(int i = 0; i < N; i++)
        par[i] = i, vis[i] = false;
}

int find(int x){
    if(par[x] != x) par[x] = find(par[x]);
    return par[x];
}

bool Union(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx == fy) return false;
    par[fx] = fy;
    return true;
}

int Kruscal(){
    int ne = 0, ans = 0;
    sort(edge, edge + m);
    for(int i = 0; i < m; i++)
        if(Union(edge[i].a, edge[i].b)){
            ans += edge[i].w;
            ne++;
            vis[i] = true;
            lca.addEdge(lca.thead, lca.tedge, edge[i].a, edge[i].b, edge[i].w, lca.te);
            if(ne == n - 1) break;
        }
    if(ne == n - 1) return ans;
    return -1;
}

int Ckruscal(){
    int res = M, me = 0, ne = 0;
    for(int i = 0; i < m; i++)
        if(!vis[i]) lca.addEdge(lca.qhead, lca.qedge, edge[i].a, edge[i].b, me++, lca.qe);
    lca.dfs(1);
    for(int i = 0; i < m; i++)
        if(!vis[i]){
            if(edge[i].w - lca.ans[ne] < res) res = edge[i].w - lca.ans[ne];
            ne++;
        }
    if(res < M) return res;
    return -1;
}

int main(){
    //clock_t start = clock();
    int t;
    scanf("%d", &t);
    for(int j = 1; j <= t; j++){
        //printf("Case %d: ", j);
        scanf("%d%d", &n, &m);
        int a, b, w;
        init();
        lca.init();
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &a, &b, &w);
            edge[i].a = a, edge[i].b = b, edge[i].w = w;
        }
        int ans = Kruscal();
        if(ans == -1){
            printf("%d\n", ans);
            continue;
        }else{
            int res = Ckruscal();
            printf("%d %d\n", ans, res == -1 ? -1 : ans + res);
        }
    }
    //clock_t stop = clock();
    //printf("Time = %.2lfMS\n", (double)(stop - start) / CLOCKS_PER_SEC * 1000);
    return 0;
}
复杂度分析

效率分析：可以证明，如果每次都选取点少的连通块，Kruskal算法求次小生成树的时间复杂度为O(M*(logN+logM))，空间复杂度为O(M)。
总结：显然Prim适用于稠密图，而Kruskal适用于稀疏图。

生成树个数

Matrix-Tree定理(Kirchhoff矩阵-树定理)。Matrix-Tree定理是解决生成树计数问题最有力的武器之一。它首先于1847年被Kirchhoff证明。在介绍定理之前，我们首先明确几个概念：

  1. G的度数矩阵D[G]是一个n*n的矩阵，并且满足：当i≠j时,dij=0；当i=j时，dij等于vi的度数。
  2. G的邻接矩阵A[G]也是一个n*n的矩阵， 并且满足：如果vi、vj之间有边直接相连，则aij=1，否则为0。
    我们定义G的Kirchhoff矩阵(也称为拉普拉斯算子)C[G]为$C[G]=D[G]-A[G]$，则Matrix-Tree定理可以描述为：G的所有不同的生成树的个数等于其Kirchhoff矩阵C[G]任何一个n-1阶主子式的行列式的绝对值。所谓n-1阶主子式，就是对于r(1≤r≤n)，将C[G]的第r行、第r列同时去掉后得到的新矩阵，用Cr[G]表示。

最小生成树的个数

算法思想：

抛开“最小”的限制不看,如果只要求求出所有生成树的个数,是可以利用Matrix-Tree定理解决的; Matrix-Tree定理此定理利用图的Kirchhoff矩阵,可以在O(N3)时间内求出生成树的个数;

kruskal算法：

将图G={V,E}中的所有边按照长度由小到大进行排序,等长的边可以按照任意顺序;
初始化图G’为{V,?},从前向后扫描排序后的边,如果扫描到的边e在G’中连接了两个相异的连通块,则将它插入G’中;
最后得到的图G’就是图G的最小生成树;

由于kruskal按照任意顺序对等长的边进行排序,则应该将所有长度为L0的边的处理当作一个阶段来整体看待;

令kruskal处理完这一个阶段后得到的图为G0,如果按照不同的顺序对等长的边进行排序,得到的G0也是不同;

虽然G0可以随排序方式的不同而不同,但它们的连通性都是一样的,都和F0的连通性相同(F0表示插入所有长度为L0的边后形成的图);

在kruskal算法中的任意时刻,并不需要关注G’的具体形态,而只要关注各个点的连通性如何(一般是用并查集表示);

所以只要在扫描进行完第一阶段后点的连通性和F0相同,且是通过最小代价到达这一状态的,接下去都能找到最小生成树;

经过上面的分析,可以看出第一个阶段和后面的工作是完全独立的;

第一阶段需要完成的任务是使G0的连通性和F0一样,且只能使用最小的代价;
计算出这一阶段的方案数,再乘上完成后续事情的方案数,就是最终答案;
由于在第一个阶段中,选出的边数是一定的,所有边的长又都为L0;
所以无论第一个阶段如何进行代价都是一样的,那么只需要计算方案数就行了;
此时Matrix-Tree定理就可以派上用场了,只需对F0中的每一个连通块求生成树个数再相乘即可;

代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
#include <ctime>
#include <queue>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#define N 1100
using namespace std;

typedef long long LL;
const int mod = 10000;

struct Edge{
    int a, b, w;

    bool operator < (const Edge &a) const{
        return w < a.w;
    }
};

int n, m;
LL par[N], fa[N], vis[N];
LL mp[N][N], mp1[N][N];
Edge edge[N];

vector <int> vec[N];

void Swap(LL &a, LL &b){
    a = a ^ b;
    b = a ^ b;
    a = a ^ b;
}

void init(){
    scanf("%d%d", &n, &m);
    fill(mp[0], mp[N], 0);
    for(int i = 0; i <= n; i++){
        vec[i].clear();
        par[i] = i;
        vis[i] = 0;
    }
    for(int i = 0; i < m; i++)
        scanf("%d%d%d", &edge[i].a, &edge[i].b, &edge[i].w);
}

int find(int x, LL father[]){
    if(x != father[x]) father[x] = find(father[x], father);
    return father[x];

    /*
       if(x == father[x]) return x;
       return find(father[x], father);
       */
}

LL Mtree(LL a[][N], int n){
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            a[i][j] %= mod;
    int ans = 1;
    for(int i = 1; i < n; i++){
        for(int j = i + 1; j < n; j++)
            while(a[j][i]){
                int temp = a[i][i] / a[j][i];
                for(int k = i; k < n; k++)
                    a[i][k] = (a[i][k] - a[j][k] * temp) % mod;
                for(int k = i; k < n; k++)
                    Swap(a[i][k], a[j][k]);
                ans = -ans;
            }
        if(a[i][i] == 0) return 0;
        ans = ans * a[i][i] % mod;
    }
    return (ans + mod) % mod;
}

void Solve(){
    if(n == 1){
        printf("1\n");
        return;
    }
    sort(edge, edge + m);
    LL flag = -1;
    LL ans = 1;
    for(int k = 0; k <= m; k++){
        if(edge[k].w != flag || k == m){
            for(int i = 1; i <= n; i++){
                if(vis[i]){
                    LL u = find(i, fa);
                    vec[u].push_back(i);
                    vis[i] = 0;
                }
            }
            for(int i = 1; i <= n; i++){
                if(vec[i].size() > 1){
                    fill(mp1[0], mp1[n + 1], 0);
                    int len = vec[i].size();
                    for(int a = 0; a < len; a++){
                        int a1 = vec[i][a];
                        for(int b = a + 1; b < len; b++){
                            int b1 = vec[i][b];
                            mp1[a][b] = (mp1[b][a] -= mp[a1][b1]);
                            mp1[a][a] += mp[a1][b1];
                            mp1[b][b] += mp[a1][b1];
                        }
                    }
                    LL res = (LL)Mtree(mp1, len);
                    ans = (ans * res) % mod;
                    for(int a = 0; a < len; a++)
                        par[vec[i][a]] = i;
                }
            }
            for(int i = 1; i <= n; i++){
                fa[i] = par[i] = find(i, par);
                vec[i].clear();
            }
            if(k == m) break;
            flag = edge[k].w;
        }
        int a = edge[k].a;
        int b = edge[k].b;
        int a1 = find(a, par);
        int b1 = find(b, par);
        if(a1 == b1) continue;
        vis[a1] = vis[b1] = 1;
        fa[find(a1, fa)] = find(b1, fa);
        mp[a1][b1]++;
        mp[b1][a1]++;
    }
    int flag1 = 0;
    for(int i = 2; i <= n && !flag1; i++)
        if(fa[i] != fa[i - 1]) flag1 = 1;
    if(m == 0) flag1 = 1;
    printf("%lld\n", flag1 ? 0 : ans % mod);
}

int main(){
    //clock_t start = clock();
    int t;
    scanf("%d", &t);
    for(int i = 1; i <= t; i++){
        init();
        Solve();
    }
    //clock_t stop = clock();
    //printf("Time = %.2lfMS\n", (double)(stop - start) / CLOCKS_PER_SEC * 1000);
    return 0;
}

另解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <ctime>
#include <queue>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#define N 550
#define Mod 10000
using namespace std;

struct Edge{
    int a, b, w;

    friend bool operator < (const Edge &a, const Edge &b){
        return a.w < b.w;
    }
};

int par[N], fa[N], cnt[N], ne[N];
int n, m, len, from, to;
Edge edge[N];

void init(int *par, int n){
    for(int i = 0; i <= n; i++)
        par[i] = i;
}

int find(int *par, int x){
    if(par[x] != x) par[x] = find(par, par[x]);
    return par[x];
}

void dfs(int pos, int num, int &ans){
    if(num == len){
        init(fa, N);
        for(int i = 0; i < from; i++){
            int fx = find(fa, edge[i].a);
            int fy = find(fa, edge[i].b);
            if(fx != fy) fa[fy] = fx;
        }
        for(int i = 0; i < len; i++){
            int di = ne[i];
            int fx = find(fa, edge[di].a);
            int fy = find(fa, edge[di].b);
            if(fx != fy) fa[fy] = fx;
            else return;
        }
        ans++;
    }else{
        for(int i = pos; i <= to; i++){
            ne[num] = i;
            dfs(i + 1, num + 1, ans);
        }
    }
}

void solve(){
    int ans = 1;
    from = to = 0;
    init(par, n);
    edge[m].w = -1;
    cnt[0] = 0;
    for(int i = 0; i < m; i++){
        int fx = find(par, edge[i].a);
        int fy = find(par, edge[i].b);
        if(i) cnt[i] = cnt[i - 1];
        if(fx != fy){
            par[fy] = fx;
            cnt[i]++;
        }
        if(edge[i].w != edge[i + 1].w){
            if(!from) len = cnt[i];
            else len = cnt[i] - cnt[from - 1];
            if(len == 0) continue;
            to = i;
            int c = 0;
            dfs(from, 0, c);
            from = i + 1;
            ans = ans * c % Mod;
        }
    }
    if(cnt[m - 1] == n - 1) printf("%d\n", ans);
    else printf("%d\n", 0);
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        scanf("%d%d", &n, &m);
        for(int i = 0; i < m; i++)
            scanf("%d%d%d", &edge[i].a, &edge[i].b, &edge[i].w);
        sort(edge, edge + m);
        solve();
    }
    return 0;
}

最小限度生成树

简述

最小度限制生成树就是给一个图，求它的满足点vo的度数最大为k的最小生成树.

算法

  1. 将v0从图中删除，将得到m个连通分量。
  2. 对每个连通分量求最小生成树，假设m个。
  3. 从每个连通分量中找与v0关联的权值最小的边，与v0相连接，这样将得到v0的最小m度生成树
  4. 如果 k < m 那么这种树是不存在的。
  5. 如果 k >= m, 那么考虑构建 m + 1度最小生成树, 将与v0关联的且不在当前的树中的边
  6. 如果将其加入树中, 必然会存在一个环，那么删掉该环中与v0不关联的权值最大边，将得到加入该边后的最小生成树，且是m + 1的。
  7. 枚举上述 6 的边找树权值最小, 那么即是m + 1度限制的最小生成树。如果 m + 1 度最小生成树的值大于 m 度最小生成树的话直接输出当前 m 度的值即可。、
  8. 重复5.6.7，直到k 度最小生成树出现。
    由上述步骤可知，由 m 度限制生成树拓展为 m + 1 度限制生成树的过程中需要大量的重复运算, 可以运用动态规划来优化。

设 $dp(v)$ 为路径 $v_0-v$ 上与 $v_0$ 无关联且权值最大的边。定义 $father(v)$ 为 v 的父结点，动态转移方程 $$p(v)=max(dp(father(v)), w(father(v),v))$$ 边界条件为 $$dp[v_0] = -\infty, dp[v^{‘}] = -\infty | (v_0, v^{‘}) \epsilon E(T)$$

算法实现

并查集 + kruskal;
首先,每个连通分量的的最小生成树可以直接用一个循环,循环着 Kruskal 求出;
这里利用了联通分量间的独立性,对每个连通分量分别求最小生成树,和放在一起求,毫不影响;
而且 kruskral 算法保证了各连通分量边的有序性;
找最小边的时候,可以用动态规划,也可以这么做：
先走一个循环,但我们需要逆过来加边,将与 v0 关联的所有边从小到达排序;
然后将各连通分量连接起来,利用并查集可以保证每个连通分量只有一条边与 v0 相连;
由于边已经从小到达排序,故与每个连通分量相连的边就是每个连通分量与 v0 相连中的最小边;
然后求 m + 1度的最小生成树时,可以直接用DFS,最小生成树要一直求到k度,然后从中找出一个最优值;

例题 [POJ 1639]

题意：

给出m条边,每条边有两个端点和一个权值;
求这个图在满足以下条件的情况下的最小生成树:
在所有点中,有一个特殊点Park,它在求得的最小生成树中的度必须小于等于某个值;

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include <map>
#include <cstdio>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 50;
const int MAX_INT = (1 << 29);

struct Edge{
    int v, w, nxt;
};

struct Node{
    int u, v, w;

    friend bool operator < (const Node &a, const Node &b){
        return a.w < b.w;
    }
};

int pcnt;
int par[MAXN];
map <string, int> ma;
Node node[MAXN * MAXN], dp[MAXN];

int ecnt, n, m, k;
bool use[MAXN][MAXN];
Edge edge[MAXN * MAXN];
int head[MAXN], vis[MAXN], dis[MAXN];

int Min[MAXN], tmp[MAXN];

void init(){
    ma.clear();
    ecnt = pcnt = 0;
    memset(dp, -1, sizeof(dp));
    memset(use, 0, sizeof(use));
    memset(edge, 0, sizeof(edge));
    memset(node, 0, sizeof(node));
    memset(head, -1, sizeof(head));
    fill(Min, Min + MAXN, MAX_INT);
    for(int i = 0; i < MAXN; i++) par[i] = i;
}

void addEdge(int u, int v, int w){
    edge[ecnt].v = v;
    edge[ecnt].w = w;
    edge[ecnt].nxt = head[u];
    head[u] = ecnt++;
}

int getId(char s[]){
    if(ma.find(s) == ma.end()) ma[s] = ++pcnt;
    else return ma[s];
    return pcnt;
}

int Find(int x){
    if(par[x] != x) par[x] = Find(par[x]);
    return par[x];
}

bool Union(int x, int y){
    int fx = Find(x);
    int fy = Find(y);
    if(fx == fy) return false;
    par[fy] = fx;
    return true;
}

void dfs(int s, int u, int fa){
    for(int i = head[u]; i + 1; i = edge[i].nxt){
        int v = edge[i].v;
        if(v != s && v != fa && use[u][v]){
            if(dp[v].w == -1){
                if(dp[u].w > edge[i].w) dp[v] = dp[u];
                else{
                    dp[v].w = edge[i].w;
                    dp[v].u = u;
                    dp[v].v = v;
                }
            }
            dfs(s, v, u);
        }
    }
}

int kruskal(int s){
    int ans = 0;
    for(int i = 0; i < n; i++){
        if(node[i].u == s || node[i].v == s) continue;
        if(!Union(node[i].u, node[i].v)) continue;
        use[node[i].u][node[i].v] = use[node[i].v][node[i].u] = true;
        ans += node[i].w;
    }
    return ans;
}

int solve(int s){
    sort(node, node + n);
    int ans = kruskal(s);
    for(int i = head[s]; i + 1; i = edge[i].nxt){
        int v = edge[i].v;
        int belong = Find(v);
        if(Min[belong] > edge[i].w){
            tmp[belong] = edge[i].v;
            Min[belong] = edge[i].w;
        }
    }

    int degree = 0;

    for(int i = 1; i <= pcnt; i++){
        if(Min[i] != MAX_INT){
            degree++;
            use[s][tmp[i]] = use[tmp[i]][s] = true;
            ans += Min[i];
        }
    }

    for(int i = degree + 1; i <= k; i++){
        dp[s].w = -MAX_INT;
        for(int j = 2; j <= pcnt; j++)
            if(use[s][j]) dp[j].w = -MAX_INT;
        dfs(s, 1, -1);
        int temp, mi = MAX_INT;
        for(int j = head[s]; j + 1; j = edge[j].nxt){
            if(mi > edge[j].w - dp[edge[j].v].w){
                mi = edge[j].w - dp[edge[j].v].w;
                temp = edge[j].v;
            }
        }
        if(mi >= 0) break;
        use[s][temp] = use[temp][s] = true;
        int u = dp[temp].u;
        int v = dp[temp].v;
        use[u][v] = use[v][u] = false;
        ans += mi;
    }
    return ans;
}

int main(){
    while(scanf("%d", &n) != EOF){
        init();
        int u, v, w;
        char s1[50];
        char s2[50];
        ma["Park"] = ++pcnt;
        for(int i = 0; i < n; i++){
            scanf("%s%s%d", s1, s2, &w);
            u = getId(s1), v = getId(s2);
            addEdge(u, v, w);
            addEdge(v, u, w);
            node[i].u = u, node[i].v = v, node[i].w = w;
        }
        scanf("%d", &k);
        int ans = solve(1);
        printf("Total miles driven: %d\n", ans);

    }
    return 0;
}

最优比率生成树

简述

引入：传说在2005年北京现场赛的赛场上，楼教主在5分钟搞定一题后第25分钟搞定了这个题，让所有人都以为这是一道水题，带坏了全场的节奏，200多次提交只有8个人过， 最终顺利夺冠。

我们设一个顶点数为n，边数为m的无环连通图G，其中 cost[i] 表示是第i条边花费的代价，benefit[i] 表示第i条边获得的收益，现要求这个图的一个生成树，使得这棵树的总花费与总收益的比值最小。这个问题就是解决最优比率生成树的问题。在实际问题当中，我们会经常遇到如修建道路要考虑收益和开销，使得代价比最小的问题。

算法

设 $x[i]$ 等于 $1$ 或 $0$ , 表示边 $e[i]$是否属于生成树. 则我们所求的比率 $$r = sum(benefit[i] * x[i]) / \sum(cost[i] * x[i]), 0≤i<m $$ 为了使 $r$ 最大, 设计一个子问题—> 让 $$z = \sum(benefit[i] * x[i]) - r * \sum(cost[i] * x[i]) = \sum(d[i] * x[i]), 其中(d[i] = benefit[i] - l * cost[i]) $$并记为 $z(r)$ .

然后明确两个性质 :

  1. z单调递减
    证明: 因为cost为正数, 所以z随l的减小而增大.

  2. z( max(r) ) = 0
    证明: 若$$z( max(r) ) < 0$$则$$\sum(benifit[i] * x[i]) - max(r) * \sum(cost[i] * x[i]) < 0$$可化为 $$max(r) < max(r)$$ 矛盾;
    若$$z( max(r) ) >= 0$$, 根据性质1, 当 $z = 0$ 时r最大.
    这样上面的问题就转化为了求 z(r) 的零点问题, 方法有以下两个:

  3. 迭代法：由上面的分析可知：
    当 $z(r) > 0$ 时，$rate$ 值无效，而 $rateNex$ 有效且$z(rateNex) <= 0$;
    当 $z(rate) < 0$ 时，$rateNex < rate$，又 $z(rate)$ 为单调递减函数，故 $0 >= z(rateNex) > z(rate)$。
    故迭代过程向 $z(rate) == 0$ 收敛，又由有限节点的完全图其生成树只有有限个可知迭代次数必为有限值。

  4. 二分法：在定出一个搜索范围和精度之后(以$[0,MAXRATE]$为例)，我们就可以使用二分法进行搜索：对于当前的搜索区间$[low,high]$，$mid = (low + high) / 2$，根据 $z(mid)$ 的值及 $z(rate)$ 的增减性，对搜索区间进行更新：
    从而在经过有限次搜索之后便能找到所求比率。

例题 [POJ 2728]

题意:

有n个村庄要连在一起，村与村之间的长度为他们之间的水平距离，连在一起的花费是两村的高度差。现求所花费和与长度和之比最小

输入:

n 和 n 个村庄的三维坐标

输出:

花费和与长度和的最小比值

参考代码

二分法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <cmath>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define ABS(x) ((x) > 0 ? (x) : (-(x)))
using namespace std;
const double eps = 1e-4;
const int MAXN = 1010;
const int MAX_INT = (1 << 29);

struct Point{
    double x, y, h;

    double CalDis(const Point &a){
        return sqrt((a.x - x) * (a.x - x) + (a.y - y) * (a.y - y));
    }

    double CalHig(const Point &a){
        return ABS(h - a.h);
    }
};

Point a[MAXN];
int n;
double mp[MAXN][MAXN];
double dis[MAXN][MAXN]; 
double cost[MAXN][MAXN];
bool vis[MAXN];
double dist[MAXN];

double prim(int s){
    memset(vis, false, sizeof(vis));
    fill(dist, dist + MAXN, MAX_INT);
    vis[s] = true;
    dist[s] = 0;
    double mi;
    int mip = s;
    double ans = 0;
    for(int i = 0; i < n; i++)
        dist[i] = mp[s][i];
    for(int i = 1; i < n; i++){
        mi = MAX_INT;
        for(int j = 0; j < n; j++)
            if(!vis[j] && mi > dist[j]) mi = dist[j], mip = j;
        ans += mi;
        vis[mip] = true;

        for(int j = 0; j < n; j++)
            if(!vis[j] && dist[j] > mp[mip][j])
                dist[j] = mp[mip][j];
    }
    return ans;
}

bool check(double mid){
    for(int i = 0; i < n; i++){
        for(int j = i + 1; j < n; j++){
            mp[i][j] = mp[j][i] = cost[i][j] - mid * dis[i][j];
        }
    }
    double mst = prim(0);
    if(mst > eps) return true;
    else return false;
}

double solve(){
    double l = 0.0, r = 100.0, mid;
    while(r - l > eps){
        mid = (l + r) / 2.0;
        if(check(mid)) l = mid;
        else r = mid;
    }
    return l;
}

int main(){
    while(scanf("%d", &n) != EOF){
        if(!n) break;
        for(int i = 0; i < n; i++)
            scanf("%lf%lf%lf", &a[i].x, &a[i].y, &a[i].h);

        fill(dis[0], dis[MAXN], MAX_INT);

        for(int i = 0; i < n; i++)
            for(int j = i + 1; j < n; j++){
                dis[i][j] = dis[j][i] = a[i].CalDis(a[j]);
                cost[i][j] = cost[j][i] = a[i].CalHig(a[j]);
            }

        double ans = solve();

        printf("%.3f\n", ans);
    }
    return 0;
}
 牛顿迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <cmath>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define ABS(x) ((x) > 0 ? (x) : (-(x)))
using namespace std;
const double eps = 1e-5;
const int MAXN = 1010;
const double MAX_INT = (1 << 29) / 1.0;

struct Point{
    double x, y, h;

    double CalDis(const Point &a){
        return sqrt((a.x - x) * (a.x - x) + (a.y - y) * (a.y - y));
    }

    double CalHig(const Point &a){
        return ABS(h - a.h);
    }
};

int n;
int pre[MAXN];
Point a[MAXN];
double mp[MAXN][MAXN];
double dis[MAXN][MAXN]; 
double cost[MAXN][MAXN];
bool vis[MAXN];
double dist[MAXN];

double prim(){
    int s = 0;
    memset(vis, false, sizeof(vis));
    memset(pre, 0, sizeof(pre));
    fill(dist, dist + MAXN, MAX_INT);
    vis[s] = true;
    dist[s] = 0.0;
    int mip = s;
    double mi = 0.0, dissum = 0.0, costsum = 0.0;
    for(int i = 1; i < n; i++){
        for(int j = 0; j < n; j++)
            if(!vis[j] && dist[j] > mp[mip][j]){
                dist[j] = mp[mip][j];
                pre[j] = mip;
            }
        mi = MAX_INT;
        for(int j = 0; j < n; j++)
            if(!vis[j] && mi > dist[j]) mi = dist[j], mip = j;
        vis[mip] = true;
        dissum += dis[mip][pre[mip]];
        costsum += cost[mip][pre[mip]];
    }
    return costsum / dissum;
}

inline void change(double mid){
    for(int i = 0; i < n; i++)
        for(int j = i + 1; j < n; j++)
            mp[i][j] = mp[j][i] = cost[i][j] - mid * dis[i][j];
}

double solve(){
    double last = 0.0, cur = -1.0;
    while(ABS(cur - last) > eps){
        last = cur;
        change(last);
        cur = prim();
    }
    return last;
}

int main(){
    while(scanf("%d", &n) != EOF){
        if(!n) break;
        for(int i = 0; i < n; i++)
            scanf("%lf%lf%lf", &a[i].x, &a[i].y, &a[i].h);

        for(int i = 0; i < n; i++)
            for(int j = i + 1; j < n; j++){
                dis[i][j] = dis[j][i] = a[i].CalDis(a[j]);
                cost[i][j] = cost[j][i] = a[i].CalHig(a[j]);
            }
        for(int i = 0; i < n; i++)
            dis[i][i] = cost[i][i] = 0.0;
        double ans = solve();
        printf("%.3f\n", ans);
    }
    return 0;
}