基本概念
无向图
连通图和非联通图: 如果无向图 G 中任意一对顶点都是连通的,则称此图是连通图(connected graph);相反,如
果一个无向图不是连通图,则称为非连通图(disconnected graph)。对非连通图G,其极大连通子图称为连通分量(connected component,或连通分支),连通分支数记为w(G)。割顶集与连通度: 设V’是连通图G 的一个顶点子集,在G 中删去V’及与V’关联的边后图不连通,则称 V’ 是 G 的割顶集(vertex-cut set)。如果割顶集V’的任何真子集都不是割顶集,则称V’为极小割顶 集。顶点个数最小的极小割顶集称为最小割顶集。最小割顶集中顶点的个数,称作图G 的顶点连通度(vertex connectivity degree),记做κ(G),且称图G 是κ–连通图(κ–connected graph)。
割点:如果割顶集中只有一个顶点,则该顶点可以称为割点(cut-vertex),或关节点。
点双连通图:如果一个无向连通图 G 没有关节点,或者说点连通度κ(G) > 1,则称 G 为点双 连通图,或者称为重连通图。
点双连通分量:一个连通图 G 如果不是点双连通图,那么它可以包括几个点双连通分量,也 称为重连通分量(或块)。一个连通图的重连通分量是该图的极大重连通子图,在重连通分量中不存在关节点。
割边集与边连通度:设 E’ 是连通图 G 的边集的子集,在 G 中删去E’后图不连通,则称E’是G 的割边集 (edge-cut set)。如果割边集 E’ 的任何真子集都不是割边集,则称 E’ 为极小割边集。边数最小的极 小割边集称为最小割边集。最小割边集中边的个数,称作图G 的边连通度(edge connectivity degree),记做λ(G),且称图G 是λ–边连通图(λ–edge–connected graph)。
割边:如果割边集中只有一条边,则该边可以称为割边(bridge),或桥。
边双连通图:如果一个无向连通图 G 没有割边,或者说边连通度λ(G) > 1,则称G 为边双连通图。
边双连通分量:边双连通分量:一个连通图 G 如果不是边双连通图,那么它可以包括几个边双连通分量。一 个连通图的边双连通分量是该图的极大重连通子图,在边双连通分量中不存在割边。在连通图中, 把割边删除,则连通图变成了多个连通分量,每个连通分量就是一个边双连通分量。
顶点连通性与边连通性的关系:(顶点连通度、边连通度与图的最小度的关系) 设G 为无向连通图,则存在关系式:$$κ(G) ≤ λ(G) ≤ δ(G)$$
割边和割点的联系:(割边和割点的联系)设 v 是图 G 中与一条割边相关联的顶点,则 v 是 G 的割点当且仅当$$deg(v) ≥ 2$$
有向图
强连通(strongly connected):若 G 是有向图,如果对图 G 中任意两个顶点 u 和 v,既存在从 u 到 v 的路径,也存在从 v 到 u 的路径,则称该有向图为强连通有向图。对于非强连通图,其极 大强连通子图称为其强连通分量。
单连通(simply connected):若 G 是有向图,如果对图 G 中任意两个顶点 u 和 v,存在从 u 到 v 的路径或从 v 到 u 的路径,则称该有向图为单连通有向图。
弱连通(weak connected):若 G 是有向图,如果忽略图 G 中每条有向边的方向,得到的无向 图(即有向图的基图)连通,则称该有向图为弱连通有向图。
无向图点连通性的求解及应用
求割点
Tarjan 算法只需从某个顶点出发进行一次遍历,就可以求得图中所有的关节点,因此其复杂度为O(n^2)。接下来以图(a)所示的无向图为例介绍这种方法。
在图(a)中,对该图从顶点 4 出发进行深度优先搜索,实线表示搜索前进方向,虚线表示 回退方向,顶点旁的数字标明了进行深度优先搜索时各顶点的访问次序,即深度优先数。在 DFS 搜索过程中,可以将各顶点的深度优先数记录在数组dfn 中。 图(b)是进行DFS 搜索后得到的根为顶点4 的深度优先生成树。为了更加直观地描述树形结 构,将此生成树改画成图(d)所示的树形形状。在图(d)中,还用虚线画出了两条虽然属于图G、但 不属于生成树的边,即(4, 5)和(6, 8)。 请注意:在深度优先生成树中,如果u 和v 是2 个顶点,且在生成树中u 是v 的祖先,则必 有dfn[u] < dfn[v],表明u 的深度优先数小于v,u 先于 v 被访问。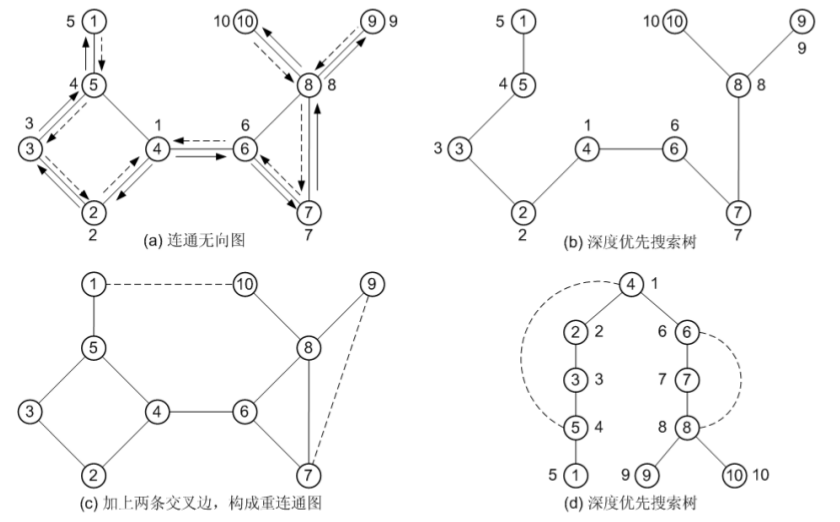
图G 中的边可以分为3 种:
- 生成树的边,如(2, 4)、(6, 7)等。
- 回边(back edge):图(d)中虚线所表示的非生成树的边,称为回边。当且仅当 u 在生成树中是 v 的祖先,或者 v 是 u 的祖先时,非生成树的边(u,v)才成为一条回边。如图(a)及图(d)中的(4, 5)、(6, 8)都是回边。
- 交叉边:除生成树的边、回边外,图G 中的其他边称为交叉边。
请特别注意:一旦生成树确定以后,那么原图中的边只可能是回边和生成树的边,交叉边实际上是不存在的。为什么?(说明:对有向图进行DFS 搜索后,非生成树的边可能是交叉边) 假设图G 中存在边(1, 10),如图(c)所示,这就是所谓的交叉边,那么顶点10(甚至其他顶点都)只能位于顶点4 的左边这棵子树中。另外,如果在图G 中增加两条交叉边(1, 10)和(7, 9),则图G 就是一个重连通图,如图(c)所示。
- 交叉边:除生成树的边、回边外,图G 中的其他边称为交叉边。
顶点u 是关节点的充要条件:
- 如果顶点u 是深度优先搜索生成树的根,则u 至少有2 个子女。为什么呢?因为删除u,它的子女所在的子树就断开了,你不用担心这些子树之间(在原图中)可能存在边,因为交叉边是不存在的。
- 如果 u 不是生成树的根,则它至少有一个子女 w,从 w 出发,不可能通过w、w 的子孙,以及一条回边组成的路径到达 u 的祖先。为什么呢?这是因为如果删除顶点 u 及其 所关联的边,则以顶点 w 为根的子树就从搜索树中脱离了。例如,顶点6 为什么是关节 点?这是因为它的一个子女顶点,如图(d)所示,即顶点7,不存在如前所述的路径到达顶点6 的祖先结点,这样,一旦顶点6 删除了,则以顶点7 为根结点的子树就断开了。 又如,顶点7 为什么不是关节点?这是因为它的所有子女顶点,当然在图(d)中只有顶点 8,存在如前所述的路径到达顶点7 的祖先结点,即顶点6,这样,一旦顶点7 删除了, 则以顶点8 为根结点的子树仍然跟图G 连通。
因此,可对图 G 的每个顶点 u 定义一个 low 值:low[u]是从 u 或 u 的子孙出发通过回边可以到达的最低深度优先数。low[u]的定义如下:
low[u] = Min
{
dfn[u],
Min{ low[w] | w 是u 的一个子女}, (8-2)
Min{ dfn[v] | v 与u 邻接,且(u,v)是一条回边 }
}
即low[u]是取以上三项的最小值,其中:
- 第1 项为它本身的深度优先数;
- 第2 项为它的(可能有多个)子女顶点w 的low[w]值的最小值,因为它的子女可以到达的最低深度优先数,则它也 可以通过子女到达;
- 第 3 项为它直接通过回边可以到达的最低优先数。
因此,顶点u 是关节点的充要条件是:u 或者是具有两个以上子女的深度优先生成树的根, 或者虽然不是一个根,但它有一个子女w,使得 low[w]>=dfn[u]。
其中,“low[w]>=dfn[u]”的含义是:顶点u 的子女顶点w,能够通过如前所述的路径到达顶 点的最低深度优先数大于等于顶点u 的深度优先数(注意在深度优先生成树中,顶点m 是顶点n 的祖先,则必有dfn[m] < dfn[n]),即w 及其子孙不存在指向顶点u 的祖先的回边。这时删除顶点 u 及其所关联的边,则以顶点 w 为根的子树就从搜索树中脱离了。 每个顶点的深度优先数dfn[n]值可以在搜索前进时进行统计,而low[n]值是在回退的时候进行计算的。
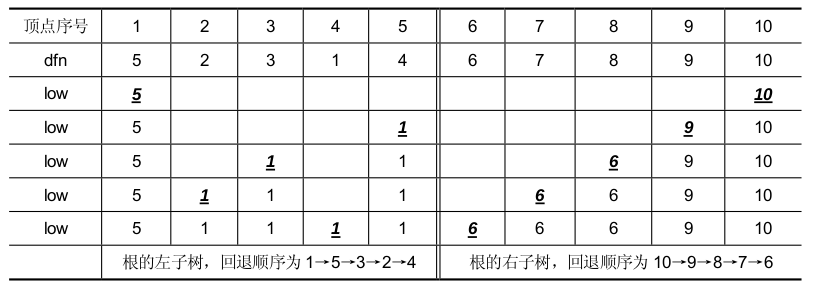
接下来结合图和表解释在回退过程中计算每个顶点 n 的low[n]值的方法 (当前计算出来的low[n]值用粗体、斜体及下划线标明):
- 在图(a)中,访问到顶点1 后,要回退,因为顶点1 没有子女顶点,所以low[1]就等于它的深度优先数dfn[1],为5;
- 从顶点1 回退到顶点5 后,要继续回退,此时计算顶点5 的low 值,因为顶点5 可以直接通过回边(5, 4)到达根结点,而根结点的深度优先数为1,所以顶点5 的low 值为1;
- 从顶点5 回退到顶点3 后,要继续回退,此时计算顶点3 的low 值,因为它的子女顶点, 即顶点5 的low 值为1,则顶点3 的low 值也为1;
- 从顶点3 回退到顶点2 后,要继续回退,此时计算顶点2 的low 值,因为它的子女顶点, 即顶点3 的low 值为1,则顶点2 的low 值也为1;
- 从顶点2 回退到顶点4 后,要继续访问它的右子树中的顶点,此时计算顶点4 的low 值,因为它的子女顶点,即顶点2 的low 值为1,则顶点4 的low 值也为1; 根结点4 右子树在回退过程计算顶点的low[n],方法类似。
求出关节点u 后,还有一个问题需要解决:去掉该关节点u,将原来的连通图分成了几个连通分量?答案是:
- 从顶点2 回退到顶点4 后,要继续访问它的右子树中的顶点,此时计算顶点4 的low 值,因为它的子女顶点,即顶点2 的low 值为1,则顶点4 的low 值也为1; 根结点4 右子树在回退过程计算顶点的low[n],方法类似。
- 如果关节点 u 是根结点,则有几个子女,就分成了几个连通分量;
- 如果关节点 u 不是根结点,则有 d 个子女 w ,使得low[w] >= dfn[u],则去掉该结点,分成了d + 1 个连通分量。
1 | // 当 res[i] > 0 时说明 i 是割点, 并且去掉 i 之后图的连通分量的个数为 res[i]; |
点双连通分量的求解
在求关节点的过程中就能顺便把每个重连通分量求出。方法是:建立一个栈,存储当前重连通分量,在 DFS 过程中,每找到一条生成树的边或回边,就把这条边加入栈中。如果遇到某个顶点 u 的子女顶点 v 满足 dfn[u] <= low[v],说明 u 是一个割点,同时把边从栈顶一条条取出,直到遇到了边(u, v),取出的这些边与其关联的顶点,组成一个重连通分量。割点可以属于多个重连通分量,其余顶点和每条边属于且只属于一个重连通分量。
1 | // bcc_cnt 即连通分支数目 |
顶点连通度求解
待补充。。。。
割边的求解
割边的求解过程与求割点的过程类似,判断方法是:无向图中的一条边(u, v)是桥,当且仅当(u, v)为生成树中的边,且满足dfn[u] < low[v]。
例如,图(a)所示的无向图,如果从顶点 4 开始进行DFS 搜索,各顶点的 dfn[] 值和 low[] 值如图(a)所示(每个顶点旁的两个数值分别表示 dfn[] 值和 low[] 值),深度优先搜索树如图(b)所 示。根据上述判断方法,可判断出边(1, 5)、(4, 6)、(8, 9)和(9, 10)为无向图中的割边。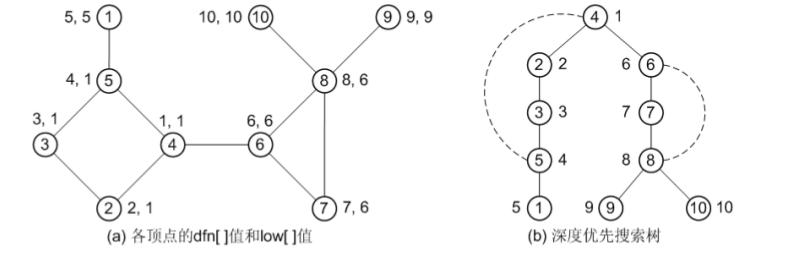
1 | // 求桥的模板, res数组存储的是桥的编号 |
边双连通分量的求解
在求出所有的桥以后,把桥删除,原图变成了多个连通块,则每个连通块就是一个边双连通分量。桥不属于任何一个边双连通分量,其余的边和每个顶点都属于且只属于一个边双连通分量。
边连通度的求解
有向图强连通性的求解及应用
有向图强连通分量的求解算法
Tarjan 算法
Tarjan 算法是基于 DFS 算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索 树中未处理的节点加入一个栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。当 dfn(u) = low(u)时,以 u 为根的搜索子树上所有节点是一个强连通分量。
接下来以图(a)所示的有向图为例解释 Tarjan 算法的思想和执行过程,在该有向图中,{ 1, 2, 5, 3 }为一个强连通分量,{ 4 }、{ 6 }也分别是强连通分量。 图(b)为从顶点1 出发进行深度优先搜索后得到的深度优先搜索树。约定:如果某个顶点有多 个未访问过的邻接顶点,按顶点序号从小到大的顺序进行选择。各顶点旁边的两个数值分别为顶 点的深度优先数(dfn[])值和low[]值。在图(b)中,虚线表示非生成树的边,其中边<5, 6>为交 叉边,边<5, 1>和<3, 5>是回边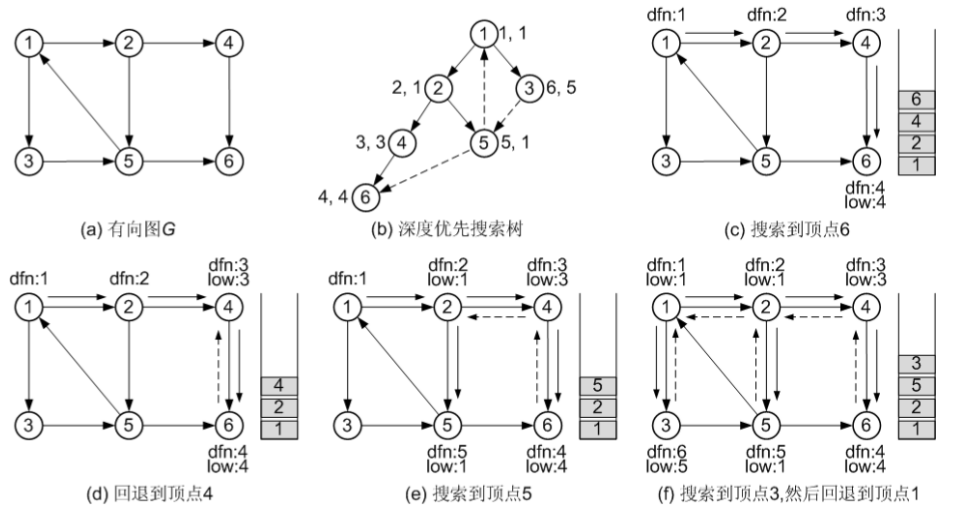
图(c)~(f)演示了 Tarjan 算法的执行过程。在图(c)中,沿着实线箭头所指示的方向搜索到顶点 6,此时无法再前进下去了,并且因为此时 dfn[6] = low[6] = 4,所以找到了一个强连通分量。退栈到u == v 为止,{ 6 }为一个强连通分量。
在图(d)中,沿着虚线箭头所指示的方向回退到顶点4,发现dfn[4] == low[4],为3,退栈后{ 4 } 为一个强连通分量。
在图(e)中,回退到顶点2 并继续搜索到顶点5,把顶点5 加入栈。发现顶点5 有到顶点 1 的有向边,顶点 1 还在栈中,所以 low[5] = 1,有向边 <5, 1> 为回边。顶点 6 已经出栈,所以 <5, 6> 是交叉边,返回顶点 2,<2, 5>为生成树的边,所以low[2] = low[5] = 1。
在图(f)中,先回退到顶点 1,接着访问顶点 3。发现顶点 3 到顶点有一条有向边,顶点 5 已经访问过了、且 5 还在栈中,因此边 <3, 5> 为回边,所以low[3] = dfn[5] = 5。返回顶点 1 后,发现 dfn[1] == low[1],把栈中的顶点全部弹出,组成一个连通分量{ 3, 5, 2, 1 }。 至此,Tarjan 算法结束,求出了图中全部的三个强连通分量为{ 6 }、{ 4 }和{ 3, 5, 2, 1 }。
Tarjan 算法的时间复杂度分析:假设用邻接表存储图,在 Tarjan 算法的执行过程中,每个顶点都被访问了一次,且只进出了一次栈,每条边也只被访问了一次,所以该算法的时间复杂度为 O(n + m)。
1 | // 代码模板 |
Kosaraju 算法
Kosaraju 算法是基于对有向图 G 及其逆图 GT(各边反向得到的有向图)进行两次 DFS 的方 法,其时间复杂度也是 O(n + m)。与 Trajan 算法相比,Kosaraju 算法的思想更为直观。
Kosaraju 算法的原理为:如果有向图 G 的一个子图 G’ 是强连通子图,那么各边反向后没有任何影响,G’ 内各顶点间仍然连通,G’ 仍然是强连通子图。但如果子图G’是单向连通的,那么各边反向后可能某些顶点间就不连通了,因此,各边的反向处理是对非强连通块的过滤。
Kosaraju 算法的执行过程为:
- (1) 对原图G 进行深度优先搜索,并记录每个顶点的 dfn[] 值。
- (2) 将图G 的各边进行反向,得到其逆图GT。
- (3) 选择从当前dfn[ ]值最大的顶点出发,对逆图GT 进行DFS 搜索,删除能够遍历到的顶点,这些顶点构成一个强连通分量。
- (4) 如果还有顶点没有删除,继续执行第(3)步,否则算法结束。
接下来以图(a)所示的有向图 G 为例分析 Kosaraju 算法的执行过程。图(b)为正向搜索过程,搜索完毕后,得到各顶点的 dfn[ ]值。图(c)为逆图GT。图(d)为从顶点3 出发对逆图GT 进行 DFS 搜索,得到第1 个强连通分量{ 1, 2, 5, 3 },图(e)和(f)分别从顶点4 和6 出发进行DFS 搜索得到另外两个强连通分量。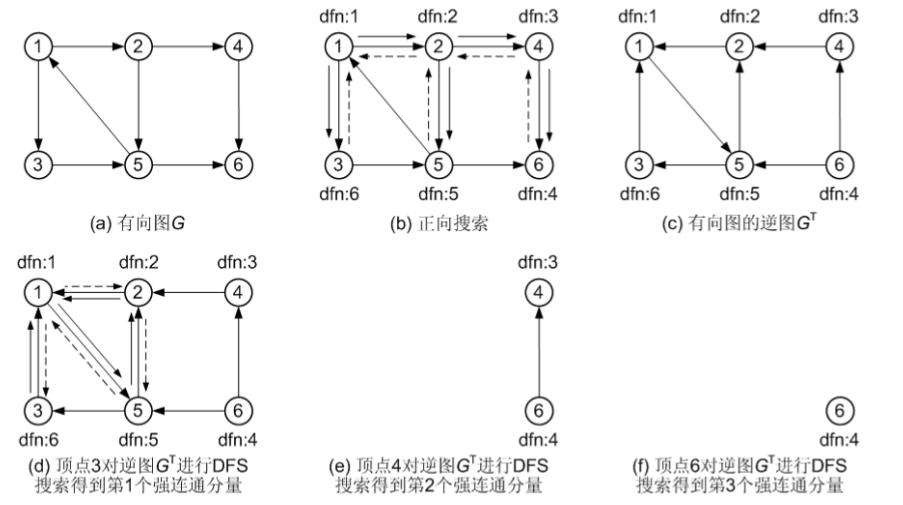
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28// 算法模板
void dfs(int u){
vis[u] = true;
for(int i = head[u]; i + 1; i = edge[i].nxt)
if(!vis[edge[i].v]) dfs(edge[i].v);
vs[vscnt++] = u;
}
void rdfs(int u, int k){
vis[u] = true;
belong[u] = k;
for(int i = rhead[u]; i + 1; i = redge[i].nxt)
if(!vis[redge[i].v]) rdfs(redge[i].v, k);
}
int scc(){
memset(vis, 0, sizeof(vis));
vscnt = 0;
for(int i = 1; i <= n; i++)
if(!vis[i]) dfs(i);
int scc_cnt = 0;
memset(vis, 0, sizeof(vis));
for(int i = vscnt - 1; i >= 0; i--)
if(!vis[vs[i]]) rdfs(vs[i], scc_cnt++);
return scc_cnt;
}连通性算法的应用2_SAT
简介
现有一个由 N 个布尔值组成的序列 A,给出一些限制关系,比如 A[x] AND A[y]=0 A[x] OR A[y] OR A[z] = 1 等,要确定 A[0..N-1] 的值,使得其满足所有限制关系。这个称为 SAT 问题,特别的,若每种限制关系中最多只对两个元素进行限制,则称为 2-SAT 问题。
展开
由于在2-SAT问题中,最多只对两个元素进行限制,所以可能的限制关系共有11种:
A[x]
NOT A[x]
A[x] AND A[y]
A[x] AND NOT A[y]
A[x] OR A[y]
A[x] OR NOT A[y]
NOT (A[x] AND A[y])
NOT (A[x] OR A[y])
A[x] XOR A[y]
NOT (A[x] XOR A[y])
A[x] XOR NOT A[y]
进一步,A[x] AND A[y]相当于(A[x]) AND (A[y])(也就是可以拆分成A[x]与A[y]两个限制关系),NOT(A[x] OR A[y])相当于NOT A[x] AND NOT A[y](也就是可以拆分成NOT A[x]与NOT A[y]两个限制关系)。因此,可能的限制关系最多只有9种。
在实际问题中,2-SAT问题在大多数时候表现成以下形式:有N对物品,每对物品中必须选取一个,也只能选取一个,并且它们之间存在某些限制关系(如某两个物品不能都选,某两个物品不能都不选,某两个物品必须且只能选一个,某个物品必选)等,这时,可以将每对物品当成一个布尔值(选取第一个物品相当于0,选取第二个相当于1),如果所有的限制关系最多只对两个物品进行限制,则它们都可以转化成9种基本限制关系,从而转化为2-SAT模型。
建模
其实 2-SAT 问题的建模是和实际问题非常相似的。建立一个 2N 阶的有向图,其中的点分为 N 对,每对点表示布尔序列 A 的一个元素的 0、1 取值(以下将代表 A[i] 的 0 取值的点称为 i,代表 A[i] 的 1 取值的点称为i’)。显然每对点必须且只能选取一个。然后,图中的边具有特定含义。若图中存在边 <i, j>,则表示若选了 i 必须选 j。可以发现,上面的 9 种限制关系中,后7种二元限制关系都可以用连边实现,比如NOT(A[x] AND A[y])需要连两条边<x, y’>和<y, x’>,A[x] OR A[y]需要连两条边<x’, y>和<y’, x>。而前两种一元关系,对于A[x](即x必选),可以通过连边<x’, x>来实现,而NOT A[x](即x不能选),可以通过连边<x, x’>来实现。
O(NM)算法:求字典序最小的解
根据 2-SAT 建成的图中边的定义可以发现,若图中 i 到 j 有路径,则若 i 选,则 j 也要选;或者说,若 j 不选,则 i 也不能选;
因此得到一个很直观的算法:
(1)给每个点设置一个状态 V,V = 0 表示未确定,V = 1 表示确定选取,V = 2 表示确定不选取。称一个点是已确定的当且仅当其 V 值非 0。设立两个队列 Q1 和 Q2,分别存放本次尝试选取的点的编号和尝试不选的点的编号。
(2)若图中所有的点均已确定,则找到一组解,结束,否则,将 Q1、Q2 清空,并任选一个未确定的点 i,将 i 加入队列 Q1,将 i’ 加入队列 Q2;
(3)找到 i 的所有后继。对于后继 j,若 j 未确定,则将 j 加入队列 Q1;若 j’(这里的 j’ 是指与 j 在同一对的另一个点)未确定,则将 j’ 加入队列 Q2;
(4)遍历 Q2 中的每个点,找到该点的所有前趋(这里需要先建一个补图),若该前趋未确定,则将其加入队列 Q2;
(5)在(3)(4)步操作中,出现以下情况之一,则本次尝试失败,否则本次尝试成功:
- <1>某个已被加入队列 Q1 的点被加入队列 Q2;
- <2>某个已被加入队列 Q2 的点被加入队列 Q1;
- <3>某个 j 的状态为 2;
- <4>某个 i’ 或 j’ 的状态为 1 或某个 i’ 或 j’ 的前趋的状态为 1 ;
(6)若本次尝试成功,则将Q1中的所有点的状态改为1,将Q2中所有点的状态改为2,转(2),否则尝试点i’,若仍失败则问题无解。
该算法的时间复杂度为 O(NM)(最坏情况下要尝试所有的点,每次尝试要遍历所有的边),但是在多数情况下,远远达不到这个上界。
具体实现时,可以用一个数组 vst 来表示队列 Q1 和 Q2。设立两个标志变量 i1 和 i2(要求对于不同的 i,i1 和 i2 均不同,这样可以避免每次尝试都要初始化一次,节省时间),若 vst[i] = i1 则表示 i 已被加入 Q1,若 vst[i] = i2 则表示 i 已被加入 Q2。不过 Q1 和 Q2 仍然是要设立的,因为遍历(BFS)的时候需要队列,为了防止重复遍历,加入 Q1(或Q2)中的点的 vst 值必然不等于 i1(或i2)。中间一旦发生矛盾,立即中止尝试,宣告失败。
该算法虽然在多数情况下时间复杂度到不了 O(NM),但是综合性能仍然不如下面的 O(M) 算法。不过,该算法有一个很重要的用处:求字典序最小的解!
如果原图中的同一对点编号都是连续的(01、23、45……)则可以依次尝试第 0 对、第 1 对……点,每对点中先尝试编号小的,若失败再尝试编号大的。这样一定能求出字典序最小的解(如果有解的话),因为一个点一旦被确定,则不可更改。
如果原图中的同一对点编号不连续(比如03、25、14……)则按照该对点中编号小的点的编号递增顺序将每对点排序,然后依次扫描排序后的每对点,先尝试其编号小的点,若成功则将这个点选上,否则尝试编号大的点,若成功则选上,否则(都失败)无解。
1 | // 模板代码 |
只输出一组可行解(O(n + m))
根据《挑战程序设计竞赛》的说法,如果不存在 x 与 NOTx 同在一个强连通分量, 那么对于每一个布尔变量 x , 让 $$ x 所在的强连通分量的拓扑序在 NOTx 所在的强连通分量之后 <=> x 为真 $$ 就是使得该公式的值为真的一组合适的布尔变量赋值。
一些例题
POJ 2117
未完待续。。。。

