Andrewei's Blog
0%

树状数组

发表于 更新于 分类于 ，

引入

早就听说过这个数据结构，但是他所做的事情线段树都可以做。年少无知的我以为知道了线段树就可以不去理会这个数据结构，然而每次做题，都要敲长长的线段树，心里苦啊。 不就是一个树状数组么，去看！

简介

树状数组可以做什么，树状数组可以维护一个序列的前缀和，并且在 $log(n)$ 的时间复杂度内进行更新和查询区间和。
它主要有两种操作：

  • 1> add(i, val); 将第 i 个元素加上 val, 复杂度为 $log(n)$
  • 2> sum(i); 统计 $[1, n]$ 的和

对，这些事情线段树都可以做到，那么树状数组的优势在哪，接着往下看。

详解

结构与节点含义

树状数组的结构是由线段树的结构简化而来，也就是说他的结构是线段树的结构的一部分，如图所示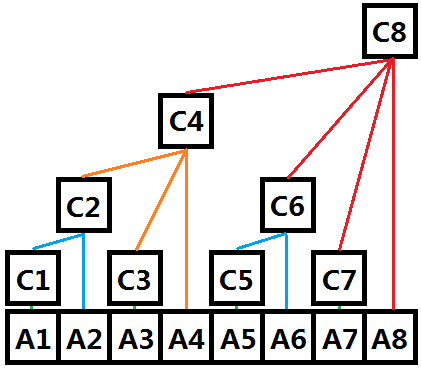树状数组的结构其中，A为普通数组，C为树状数组。
下面我们来看一下树状数组每个节点的含义:

节点 下标二进制 含义
C1 0001 C1 = A1
C2 0010 C2 = C1 + A2 = A1 + A2
C3 0011 C3 = A3
C4 0100 C4 = C2 + C3 + A4 = A1 + … + A4
C5 0101 C5 = A5
C6 0110 C6 = C5 + A6 = A5 + A6
C7 0111 C7 = A7
C8 1000 C8 = C4 + C6 + C7 + A8 = A1 + … + A8

通过观察表格我们发现，树状数组里面的每一个节点其实代表的都是一个区间的和，设有一个下标为 $i$ 的节点 $C_i$, 并且假定 $i$ 的二进制表示中末尾有 $k$ 个 $0$, 则, $C_i$ 代表的是从第 $i$ 个数向前数 $2^k$ 个数的和，即 $C_i$为:

$$\sum_{j=i-2^k+1}^{i}A_j$$

求和操作

在我们明白了树状数组中每个节点的含义之后，我们来构造求区间$[1, i], 1 <= i <= n$ 的和(记为sum(i))的方法，首先我们先假定 int lowbit(int i); 函数用来表示 $2^k$(其中 $k$ 为 $i$ 的二进制中末尾 $0$ 的个数)，他的实现方式我们稍后再讲。 那么:

$$ sum(i) = sum(i - lowbit(i)) + C_i$$

该式可递归求解也可迭代求解，结束的条件是 $ i <= 0 $

下面以求区间 $[1,7]$ 的和(即 sum(6)的值)为例介绍求和操作的步骤:

  • lowbit(7) = 1 即 $C_7=A_7$, 故 $sum(7)=sum(7-1)+C_7$;
  • lowbit(6) = 2 即 $C_6=A_6+A_5$, 故 $sum(6)=sum(6-2)+C_6$;
  • lowbit(4) = 4 即 $C_4=A_1+A_2+A_3+A_4$, 故 $sum(4)=sum(4-4)+C_4$;
    由于 $4-4==0$, 故算法停止，最后得知 $sum(7)=C_7+C_6+C_4$;

现在我们已经学会了求区间 $[1,n]$ 的和，对于任意的区间 $[l,r]$的和, 只需要求 $sum(r)-sum(l-1)$ 即可。

求和操作的参考代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
// 迭代求解
int getSum(int x){
    int sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        sum += C[i];
    }
    return sum;
}

// 递归求解
int getSum(int x){
    return x > 0 ? C[x] + getSum(x - lowbit(x)) : 0;
}

更新操作

介绍完了求和操作，下面介绍更新操作。上文中已经提到，树状数组中的每一个节点维护的都是一个区间和，那么当一个节点的值发生变化的时候也就意味着会有一系列与之相关的节点的值也要发生变化，这一点从树状数组的结构图中也可以看出。

比如 $C_1$ 节点发生变化，那么 $C_1, C_2, C_4, C_8, …$ 都要跟着变化，如何维护好这个变化是我们需要关注的事情。

由结构图我们知道，当一个节点变化时影响到的是本节点和该节点的直接和间接父节点，而对于一个节点 $i$, 它的父节点的下标为 i + lowbit(i), 所以更新操作跟求和操作非常相似，只需要不断的寻找父节点然后更新它即可。

更新操作参考代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 迭代求解
void update(int x, int val){
    for(int i = x; i <= n; i += lowbit(i)){
        C[i] += val;
    }
}

// 递归求解
void update(int x, int val){
    if(x <= n){
        C[x] += val;
        update(x + lowbit(x), val);
    }
}

lowbit 函数的实现

上文中我们一直在用 lowbit(x) 这个函数来求 $2^k$(其中 k 为 x 二进制表示中末尾0的个数), 那么这个函数怎么实现最方便快捷呢？
当然，完全可以用循环的方式从 x 的最后一位遍历，但是还有更好的方法，那就是 x & (-x)。
下面解释一下这个表达式为什么可以求出我们所需要的东西, 这里假定 x 为 n 位有符号整数且非负, 则：
lowbit原理

当然 lowbit 函数还可以用 ((i-1)^i)&i 来实现，都是利用了二进制的性质，这里不再解释。

lowbit函数参考代码:

1
2
3
4
5
6
7
8
9
// 实现方式1
int lowbit(int x){
    return x & (-x);
}

// 实现方式2
int lowbit(int x){
    return ((x - 1) ^ i) & i;
}

应用

讲到这里大家肯定已经感觉出树状数组的优势来了，代码简单的已经跟 a + b 差不多了，那么除了刚刚所描述的基本用法之外，哪些地方还可以巧妙地利用树状数组呢?

应用一 单点更新，区间查询

** 问题:**
一个长度为 $n(1 <= n <= 500000)$ 的元素序列，一开始都为 0，现给出三种操作:

  • add x v, 给第 x 个元素的值加上 v;
  • sub x v, 给第 x 个元素的值减去 v;
  • sum x y, 求出第 x 个元素到第 y 个元素的和;

解答:
这是最基本的树状数组的用法，前两种操作都可以直接使用 update(x, v);来实现，第三种操作就用 getSum(y) - getSum(x - 1)来实现

应用二 区间更新，单点查询

问题:
一个长度为 $n(1 <= n <= 500000)$ 的元素序列，一个开始都为 0, 现给出两种操作:

  • add x y v, 给第 x 个元素到第 y 个元素的值都加上 v;
  • get x, 查询第 x 个元素的值;

解答:
这个问题可以转换到单点更新，区间查询上去，转换方法如下:
第一种操作，我们用两步 update 来实现, 分别为 update(x, v) 和 update(y + 1, -v);
第二种操作, 查询第 x 个元素的值时，直接调用 getSum(x) 即可。

注意: 此时 getSum(x) 得到的其实是 x 元素的 增量。

拓展:
如果原始数据不为 0, 则 get x 时应当写为 getSum(x) + data[x], 其中 data[x] 为第 x 个元素的初始值。

应用三 区间更新，区间查询

问题:
一个长度为 $n(1 <= n <= 500000)$ 的元素序列，现给出两种操作:

  • add x y v, 给第 x 个元素到第 y 个元素的值都加上 v;
  • sum x y, 求出第 x 个元素到第 y 个元素的和;

解答:
首先说明树状数组是可以解决这个问题的，但是感觉这种问题已经违背了树状数组的本意，所以建议这种问题用线段树来做。
下面介绍树状数组的做法:
设 $s(i) = $加上 $v$ 之前的 $\sum_{j=1}^{i}a_j$

设 $s’(i) = $加上 $v$ 之后的 $\sum_{j=1}^{i}a’_j$
那么:

$i < x : s’(i) = s(i)$

$x <= i <= y : s’(i) = s(i) + v * (i - x + 1)$

$y < i : s’(i) = s(i) + v * (y - x + 1)$

我们构建两个树状数组 bit0, bit1，并且满足：
$$\sum_{j=1}^{i}a_j = sum(bit1, i) * i + sum(bit0, i)$$
于是，在区间 $[l,r]$ 上同时加上 $x$ 就可以看作是:

在 bit0 上的 l 位置上加上 -x(l-1)
在 bit1 上的 l 位置上加上 x
在 bit0 上的 r+1 位置上加上 x*r
在 bit1 上的 r+1 位置上加上 -x

这四个操作都可以在 $log(n)$ 内完成。
下面实现一下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int n;
int a[MAXN];                // 原始数据
int bit0[MAXN], bit1[MAXN];

int lowbit(int x){
    return x & (-x);
}

int getSum(int *bit, int x){
    int sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        sum += bit[i];
    }
    return sum;
}

int update(int *bit, int x, int val){
    for(int i = x; i <= n; i += lowbit(i)){
        bit[i] += val;
    }
}

void solve(){
    for(int i = 1; i <= n; i++){
        update(bit0, i, a[i]);
    }

    // 更新操作 [x, y] 区间内加上 val;
    update(bit0, x, -val * (x - 1));
    update(bit1, x, val);
    update(bit0, y + 1, val * y);
    update(bit1, y + 1, -val);

    // 求和操作 求 [x, y] 区间和
    int sum = 0;
    sum += getSum(bit0, y) + getSum(bit1, y) * y;
    sum -= getSum(bit0, x - 1) + getSum(bit1, x - 1) * (x - 1);
}

应用四 求逆序对数

问题1:
一个长度为 $n(1 <= n <= 500000)$ 的元素序列，给定每个数的值, 求它的逆序对数

解答:
求逆序对可以用 归并排序 来解，复杂度为 $nlog(n)$, 如果用树状数组的话, 怎么做呢?
我们用一个例子来介绍求解的步骤，比如我们要求 4, 2, 1, 3, 6, 5 这个序列的逆序对。

首先，我们要声明一个数组，初始化为 0, 大小为我们要求的那个序列的最大值(如果最大值太大的话，建议离散化), 并将答案记录在 ans 中;

  1. 将 4 插入到序列中，执行 update(4, 1), cnt += (1 - getSum(4));
  2. 将 2 插入到序列中，执行 update(2, 1), cnt += (2 - getSum(2));
  3. 将 1 插入到序列中，执行 update(1, 1), cnt += (3 - getSum(1));
  4. 将 3 插入到序列中，执行 update(3, 1), cnt += (4 - getSum(3));
  5. 将 6 插入到序列中，执行 update(6, 1), cnt += (5 - getSum(6));
  6. 将 5 插入到序列中，执行 update(5, 1), cnt += (6 - getSum(5));
    当这些操作做完后，cnt 就是我们要求的值.

问题2:
给定$N(N <= 100000)$个区间，定义两个区间$(S_i, E_i)$和$(S_j, E_j)$的>如下：如果 $S_i <= S_j and E_j <= E_i and E_i - S_i > E_j - S_j$,则 $(S_i, E_i) > (S_j, E_j)$，现在要求每个区间有多少区间>它。
简化这个问题的话就是求, 有多少个区间 $i$ 完全覆盖 $j$, 并且这两个区间不能相等(如下图所示)。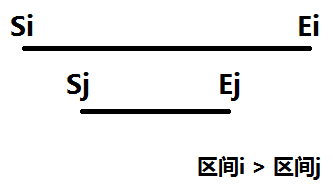
应用四题目
解答:

  1. 对区间进行排序，排序规则为：左端点递增，如果左端点相同，则右端点递减。
  2. 枚举区间，不断插入区间右端点，因为区间左端点是保持递增的，所以对于某个区间$(S_i, E_i)$，只需要查询树状数组中$[Ei, MAX]$这一段有多少已经插入的数据，就能知道有多少个区间是比它大的，这里需要注意的是多个区间相等的情况，因为有排序，所以它们在排序后的数组中一定是相邻的，所以在遇到有相等区间的情况，需要”延迟”插入。等下一个不相等区间出现时才把之前保存下来的区间右端点进行插入。插入完毕再进行统计。
    备注: 这里的插入即$(E_j, 1)$，统计则是$getSum(n) - getSum(E_i - 1)$ (其中 $j < i$ )。

关于逆序对的种种讨论

既然提到了逆序对，那么我们现在来讨论一下当一个序列发生改变时其逆序对的变化

问题1:

现在考虑这样一个问题：在序列 $a[]$ 中，交换 $a[i]$ 与 $a[j](i < j)$，则序列的逆序对数奇偶性有何变化？

解答:

为了简化问题，我们首先考虑 $i, j$ 相邻的情况:
我们可以肯定的是如果 $i, j$ 相邻， 那么 $a[i], a[j]$ 的交换不会引起 $a[k], k < i$ 和 $a[k], k > j$ 的逆序对, 那么: 当 $a[i] > a[j]$时，$a[i], a[j]$ 的交换会导致整体的逆序对数 $-1$, 反之会导致整体的逆序对数 $+1$, 也就是说 ** $a[i], a[j]$ 的交换会导致整体逆序对数的变化，即相邻两个数的交换会导致整体逆序对数的变化 **(在这里我们不考虑 $a[i] == a[j]$)。
假设 $a[i]$ 与 $a[j]$ 之间有 $m(m >= 1)$ 个数:
这种情况下，我们可以考虑 $a[i], a[j]$ 的交换是下面三种情况的叠加,

  1. $a[i]$ 依次与其后面的 $m$ 个数交换直到 $a[j]$, 共进行 $m$ 次交换;
  2. $a[i], a[j]$ 进行交换，共$1$次;
  3. $a[j]$ 依次与其前面的 $m$ 个数交换直到 $a[i]$ 之前的位置，共进行 $m$ 次交换;

如此可知，共进行了 $2 \ast m + 1$ 次交换, 综合两种情况可知 任何两个数的交换会导致整体逆序对数的变化(不考虑 $a[i] == a[j]$ 的情况).

问题2:

在问题1的基础上我们接着考虑，$a[i], a[j]$交换后对整体逆序对数量的影响。
解答:

可以很容易的想到想要解决这个问题，必须要知道在区间 $[l, r]$ 中比 $a[i]$ 小的数的个数 num_less_i, 比 $a[i]$ 大的数的个数 num_larger_i, 比 $a[j]$ 小的数的个数 num_less_j, 比 $a[j]$ 大的数的个数 num_larger_j, 则逆序对的变化为:
change_num = -num_less_i + num_larger_i + num_less_j - num_larger_j
现在的问题是如何快速的求出这些值。
令 cnt[i][j] 表示到位置 i 为止(包括i), 比 j 小的数的个数，并且假定对任意的 $a[i], a[i] <= m$, 那么

1
2
3
4
5
num_less_i = cnt[j][a[i]] - cnt[i][a[i]];
num_larger_i = j - i - num_less_i;
num_less_j = cnt[j][a[j]] - cnt[i][a[j]];
num_larger_j = j - i  - 1 - num_less_j;
//第四行的减一是减去a[j]本身也算一个数

至于 cnt 数组可以预处理出来:

1
2
3
4
5
6
7
//递推求cnt数组, 复杂度比较大
for(int i = 1; i <= n; i++){
    for(int j = 1; j <=m; j++){
        if(a[i] < j)cnt[i][j] = cnt[i - 1][j] + 1;
        else cnt[i][j] = cnt[i - 1][j];
    }
}

问题解决.

问题3:

现在已知这样一个序列 b, $b[i], (1 <= i <= n)$ 表示 $i$ 在另外一个序列中的逆序对数，试问能否构造出这样的一个$1 - n $的排列，满足b序列？

解答:

这个问题刚好和求逆序对数反了过来。举个例子，b 序列 1 ,2 , 0, 1, 0.如何构造呢？
不妨试一试.1的逆序对数是1，也就是说，1在新序列中他的前面只能有1个比他大的数，但是1已经是最小数了，所以1必定处在第2的位置.构造序列： _ 1 _ _ 2的逆序对数是2，依照前面的分析方法，2必定处在第4的位置，即 _ 1 _ 2 。换句话说，2要找到第3个空位.再换个角度，对于位置序列（1,2,3,4,5），数字1已经占据了第2的位置，所以将序列中的2删除->(1,3,4,5)，那么我们要寻找的2的插入位置不就是第3小的元素，也就是第b[i]小元素么.求第K`小元素上面已经分析过了，树状数组可以搞定.

1
2
3
4
5
6
7
//ans为构造的序列
//c[]为位置序列
for(int i = 1; i <= n; i++){
    int pos = find_kth_element(k);
    ans[pos] = c[i];
    update(pos, -1);
}

问题4:

仍是上一题中的序列b，b[i]表示原序列中位置 i 处的逆序对数，问你能否构造出原序列？(原序列为1-n的一个排列)

解答:

此题和上一题的不同.但是可以采用和上一题的相同的思路去解决.比如b序列 0, 1, 2, 0, 1

因为一个序列的第一个数的逆序对数总是为0，所以从前往后的分析不太靠谱.那么我们试一试从后向前分析.最后一个数的逆序对数为1，说明他前面只能有一个数比他大，显然最后一个数只能是4.即序列变成 _ _ _ _ 4. 倒数第二个数的逆序对数为0，则同样可确定该数只能是5.序列变成 _ _ _5 4. 倒数第三个数的逆序对数为2，可确定该数为1.有什么规律呢？用cnt表示还剩下的数，每次要填的数，是不是第cnt - b[i]小的数呢？倒数第一个数的逆序对数为1，要填的是第 5 - 1小的数，也就是4. 然后倒数第二个数的逆序对数为0，要填第 4-0小的数，在剩余的数里面就是5.以此类推.

1
2
3
4
5
6
7
//算法伪代码
//ans为构造的序列
for(int i = n; i > 0; i--){
    int num = find_kth_element(i - b[i]);
    ans[i] = num;
    update(num, -1);
}

应用五 求第k大数

问题:

给定一个空的栈，现对他进行如下操作:

  1. push x, 将 x(0 <= x <= 1000) 放于栈顶;
  2. pop, 将栈顶元素弹出;
  3. query k, 查询栈中第 k 大元素;

解答:

开一个大小为 1000 的数组并初始化为 0,

  1. 当进行 push x 操作的时候调用 update(x, 1);
  2. 当进行 pop 操作的时候调用 update(x, -1);
  3. 对于 query k 操作，实际上就是找到一个右端点 r, 使得 $[1, r]$ 的和为 k, 故我们可以用二分与树状数组相结合来查找 r;

具体实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
const int MAXN = 1010;

int a[MAXN];
stack <int> sta;

int lowbit(int x){
    return x & (-x);
}

void update(int x, int val){
    for(int i = x; i < MAXN; i += lowbit(i)){
        a[i] += val;
    }
}

int getSum(int x){
    int sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        sum += a[i];
    }
    return sum;
}

int FindMid(int k){
    int l = 0, r = MAXN;
    while(r - l > 1){
        int mid = (l + r) >> 1;
        if(getSum(mid) < k) l = mid;
        else r = mid;
    }
    return r;
}

void solve(){

    memset(a, 0, sizeof(a));
    while(!sta.empty()) sta.pop();

    // push x 操作
    sta.push(x);
    update(x, 1);

    // pop 操作
    top = sta.top();
    update(top, -1);
    sta.pop();

    // query k 操作
    ans = Find(k);
}

应用六 二维树状数组

问题:

给定一个矩阵 $mp(n * m, (1 <= n, m <= 1000))$, 初始情况元素均为 $0$, 有两种操作:

  1. add x y v, 表示 $ mp[x][y] += v $;
  2. query x1 y1 x2 y2, 表示询问由 x1, y1, x2, y2 围成的矩形中所有数的和;

解答:

可以把普通的一维树状数组改写为二维的树状数组:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int lowbit(int x){
    return x & (-x);
}

void update(int x, int y, int val){
    for(int i = x; i <= n; i += lowbit(i)){
        for(int j = y; j <= m; j += lowbit(j)){
            c[i][j] += val;
        }
    }
}

int getSum(int x, int y){
    int sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        for(int j = y; j; j -= lowbit(j)){
            sum += c[i][j];
        }
    }
    return sum;
}

仔细观察即可发现，二维树状数组的实现和一维的实现极其相似，二维仅仅比一维多了一个循环，并且数据用二维数组实现。那么同样地，对于三维的情况，也只是在数组的维度上再增加一维，更新和求和时都各加一个循环而已。

此时，如果需要求 $(x1, y1), (x2, y2)$ 这两个点所框定的矩阵中的和则会有以下公式:
$$ sum = getSum(x2, y2) - getSum(x1 - 1, y2) - getSum(x2, y1 - 1) + getSum(x1 - 1, y1 - 1)$$

总结

罗嗦了这么多，我们来总结一下树状数组的优势:

  1. 编码复杂度极低，跟它的功能比起来性价比超高;
  2. 运用非常灵活，功能强大;
  3. 一维树状数组的各种操作的复杂度均为 $O(log(n))$;
  4. 只需要线性的空间，空间复杂度为 $O(n)$;
  5. 可以拓展成为 $n$ 维的情况.